题目内容
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线 ,在抛物线上任意画一个点
,在抛物线上任意画一个点 ,度量点
,度量点 的坐标
的坐标 ,如图.
,如图.

(Ⅰ)拖动点 ,发现当
,发现当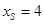 时,
时, ,试求抛物线
,试求抛物线 的方程;
的方程;
(Ⅱ)设抛物线 的顶点为
的顶点为 ,焦点为
,焦点为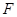 ,构造直线
,构造直线 交抛物线
交抛物线 于不同两点
于不同两点 、
、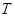 ,构造直线
,构造直线 、
、 分别交准线于
分别交准线于 、
、 两点,构造直线
两点,构造直线 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 ,无论怎样拖动点
,无论怎样拖动点 ,恒有
,恒有
 .请你证明这一结论.
.请你证明这一结论.
(Ⅲ)为进一步研究该抛物线 的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点
的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点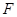 ”改变为其它“定点
”改变为其它“定点
 ”,其余条件不变,发现“
”,其余条件不变,发现“ 与
与 不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“
不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“
 ”成立?如果可以,请写出相应的正确命题;否则,说明理由.
”成立?如果可以,请写出相应的正确命题;否则,说明理由.
 ,在抛物线上任意画一个点
,在抛物线上任意画一个点 ,度量点
,度量点 的坐标
的坐标 ,如图.
,如图.
(Ⅰ)拖动点
 ,发现当
,发现当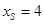 时,
时, ,试求抛物线
,试求抛物线 的方程;
的方程;(Ⅱ)设抛物线
 的顶点为
的顶点为 ,焦点为
,焦点为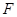 ,构造直线
,构造直线 交抛物线
交抛物线 于不同两点
于不同两点 、
、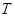 ,构造直线
,构造直线 、
、 分别交准线于
分别交准线于 、
、 两点,构造直线
两点,构造直线 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 ,无论怎样拖动点
,无论怎样拖动点 ,恒有
,恒有
 .请你证明这一结论.
.请你证明这一结论. (Ⅲ)为进一步研究该抛物线
 的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点
的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点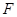 ”改变为其它“定点
”改变为其它“定点
 ”,其余条件不变,发现“
”,其余条件不变,发现“ 与
与 不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“
不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“
 ”成立?如果可以,请写出相应的正确命题;否则,说明理由.
”成立?如果可以,请写出相应的正确命题;否则,说明理由.(Ⅰ)
(Ⅱ)设出直线方程,点的坐标,联立方程组证明
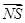 ,所以
,所以

(Ⅲ)设抛物线 的顶点为
的顶点为 ,定点
,定点 ,过点
,过点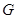 的直线
的直线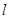 与抛物线
与抛物线 相交于
相交于 、
、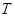 两点,直线
两点,直线 、
、 分别交直线
分别交直线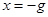 于
于 、
、 两点,则
两点,则


(Ⅱ)设出直线方程,点的坐标,联立方程组证明

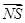 ,所以
,所以

(Ⅲ)设抛物线
 的顶点为
的顶点为 ,定点
,定点 ,过点
,过点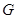 的直线
的直线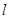 与抛物线
与抛物线 相交于
相交于 、
、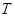 两点,直线
两点,直线 、
、 分别交直线
分别交直线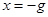 于
于 、
、 两点,则
两点,则

试题分析:解法一:(Ⅰ)把
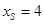 ,
, 代入
代入 ,得
,得 , 2分
, 2分所以
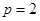 , 3分
, 3分因此,抛物线
 的方程
的方程 . 4分
. 4分(Ⅱ)因为抛物线
 的焦点为
的焦点为 ,设
,设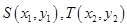 ,
,依题意可设直线
 ,
,由
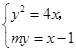 得
得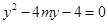 ,则
,则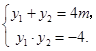 ① 6分
① 6分又因为
 ,
, ,所以
,所以 ,
, ,
,所以
 ,
, , 7分
, 7分又因为
 8分
8分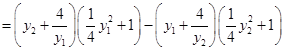


 , ②
, ②把①代入②,得
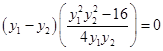 , 10分
, 10分即
 ,
,所以

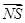 ,
,又因为
 、
、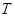 、
、 、
、 四点不共线,所以
四点不共线,所以
 . 11分
. 11分(Ⅲ)设抛物线
 的顶点为
的顶点为 ,定点
,定点 ,过点
,过点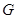 的直线
的直线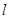 与抛物线
与抛物线 相交于
相交于 、
、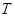 两点,直线
两点,直线 、
、 分别交直线
分别交直线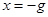 于
于 、
、 两点,则
两点,则
 . 14分
. 14分解法二:(Ⅰ)同解法一.
(Ⅱ)因为抛物线
 的焦点为
的焦点为 ,设
,设 , 5分
, 5分依题意,可设直线
 ,
,由
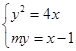 得
得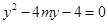 ,
,则
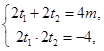
所以
 7分
7分又因为
 ,
, ,
,所以
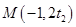 ,
, , 10分
, 10分所以
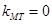 ,
, ,
, 又因为
 、
、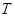 、
、 、
、 四点不共线,所以
四点不共线,所以
 . 11分
. 11分(Ⅲ)同解法一. 14分
解法三:(Ⅰ)同解法一.
(Ⅱ)因为抛物线
 的焦点为
的焦点为 ,设
,设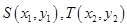 ,
,依题意,设直线
 ,
,由
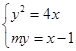 得
得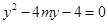 ,则
,则 , 6分
, 6分又因为
 ,
, ,所以
,所以 ,
, ,
,又因为

 , 9分
, 9分所以
 ,所以
,所以 平行于
平行于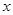 轴;
轴;同理可证
 平行于
平行于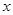 轴;
轴;又因为
 、
、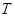 、
、 、
、 四点不共线,所以
四点不共线,所以
 . 11分
. 11分(Ⅲ)同解法一. 14分
点评:圆锥曲线问题在高考中每年必考,且一般出在压轴题的位置上,难度较低,主要考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、数形结合思想等。

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
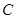 的中心在原点,焦点在
的中心在原点,焦点在 轴上,短轴的一个端点与左右焦点
轴上,短轴的一个端点与左右焦点 、
、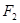 组成一个正三角形,焦点到椭圆上的点的最短距离为
组成一个正三角形,焦点到椭圆上的点的最短距离为 .
. 与椭圆
与椭圆 、
、 两点,线段
两点,线段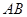 的中点为
的中点为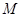 ,求直线
,求直线 的斜率
的斜率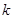 的取值范围.
的取值范围.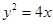 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )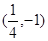
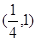
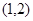
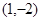
 ,两个焦点为
,两个焦点为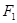 、
、 ,
, ,则双曲线的离心率为____________.
,则双曲线的离心率为____________.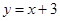 与曲线
与曲线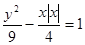 的交点的个数是 个.
的交点的个数是 个.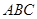 两个顶点
两个顶点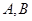 的坐标分别是
的坐标分别是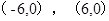 ,边
,边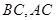 所在直线的斜率之积等于
所在直线的斜率之积等于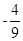 ,求顶点
,求顶点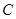 的轨迹方程,并画出草图。
的轨迹方程,并画出草图。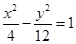 上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )  的离心率为2,则双曲线
的离心率为2,则双曲线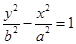 的离心率为( )
的离心率为( )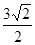
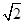

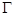 的方程为
的方程为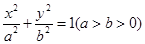 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b). ,求点
,求点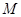 的坐标;
的坐标; 交椭圆
交椭圆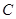 、
、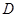 两点,交直线
两点,交直线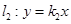 于点
于点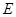 .若
.若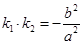 ,证明:
,证明: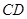 的中点;
的中点;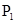 、
、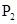 满足
满足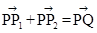 ,写出求作点
,写出求作点