题目内容
【题目】如图,四棱锥P﹣ABCD的底面是AB=2,BC= ![]() 的矩形,△PAB是等边三角形,侧面PAB⊥底面ABCD
的矩形,△PAB是等边三角形,侧面PAB⊥底面ABCD
(Ⅰ)证明:BC⊥面PAB
(Ⅱ)求侧棱PC与底面ABCD所成的角.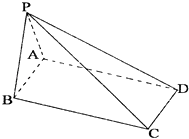
【答案】证明:(Ⅰ)∵侧面PAB垂直于底面ABCD,且侧面PAB与底面ABCD的交线是AB,
在矩形ABCD中,BC⊥AB,
∴BC⊥侧面PAB.
解:(Ⅱ)在侧面PAB内,过点P做PE⊥AB.垂足为E,连接EC,
∵侧面PAB与底面ABCD的交线是AB,PE⊥AB.
∴PE⊥底面ABCD.于是EC为PC在底面ABCD内的射影,
∴∠PCE为侧棱PC与底面ABCD所成的角,
在△PAB和△BEC中,易求得PE= ![]() ,
,
在Rt△PEC中,∠PCE=45°(12分)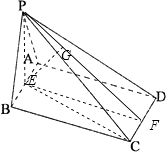
【解析】(Ⅰ)根据平面与平面垂直的性质定理,结合已知可证得BC⊥侧面PAB;(Ⅱ)在侧面PAB内,过点P做PE⊥AB.垂足为E,连接EC,根据线面所成角的定义可知∠PCE为侧棱PC与底面ABCD所成的角,在Rt△PEC中,求出此角即可.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定和平面与平面垂直的性质的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

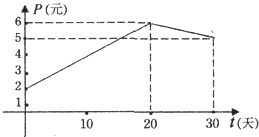
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示.
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?