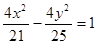题目内容
圆C1:  与圆C2:
与圆C2: 的位置关系是( )
的位置关系是( )
| A.外离 | B.外切 | C.内切 | D.相交 |
B
解析试题分析:因为|C1C2|= 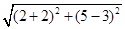 =5,R=1,r=4,|C1C2|=R+r,所以两圆外切,选B。
=5,R=1,r=4,|C1C2|=R+r,所以两圆外切,选B。
考点:本题主要考查两圆的位置关系。
点评:简单题,研究圆与圆的位置关系,由几何法和代数法两种,较常用的是几何法,研究半径之和差与圆心距之间的关系。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
直线 被圆
被圆 截得的线段的长为( )
截得的线段的长为( )
| A.2 | B. | C. | D.1 |
已知 为圆
为圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与该圆的位置关系是 ( )
与该圆的位置关系是 ( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
已知圆 和直线
和直线 相交于P,Q两点,则
相交于P,Q两点,则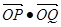 的值为(O为坐标原点)( )
的值为(O为坐标原点)( )
| A.12 | B.16 | C.21 | D.25 |
直线 与圆
与圆 相交于
相交于 ,
, 两点,若
两点,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知集合 ,
,


 。若存在实数
。若存在实数 使得
使得 成立,称点
成立,称点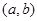 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是
内的个数是
| A.0 | B.1 | C.2 | D.无数个 |
设 ,若线段
,若线段 是△
是△ 外接圆的直径,则点
外接圆的直径,则点 的坐标是( ).
的坐标是( ).
| A.(-8,6) | B.(8,-6) | C.(4,-6) | D.(4,-3) |
若直线 (
( )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).