题目内容
已知
为圆
内异于圆心的一点，则直线
与该圆的位置关系是 （ ）
| A．相切 | B．相交 | C．相离 | D．相切或相交 |
C
解析试题分析：由圆的方程找出圆心坐标与半径，因为M为圆内一点，所以M到圆心的距离小于
圆的半径，利用两点间的距离公式表示出一个不等式，然后利用点到直线的距离公式表示出
圆心到已知直线的距离d，根据求出的不等式即可得到d大于半径r，得到直线与圆的位置关
系是相离．由圆的方程得到圆心坐标为（0，0），半径r=a，
由M为圆内一点得到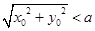
，则圆心到已知直线的距离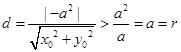
直线与该圆的位置关系是相离，故选C.
考点：直线与圆的位置关系
点评：此题考查小时掌握点与圆的位置关系及直线与圆的位置关系的判断方法，灵活运用两点间的距离公式及点到直线的距离公式化简求值，是一道综合题
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
，在上任取一点
，线段
长度的最小值称为点
．设是长为2的线段，点集
所表示图形的面积为（ ）
已知圆的方程为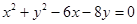
.设该圆过点H（3，5）的两条弦分别为AC和BD，且
.则四边形ABCD的面积最大值为（ ）
A． | B． | C．49 | D．50 |
若函数
的图象在x=0处的切线
与圆
相离，则
与圆C的位置关系是（ ）
| A．在圆外 | B．在圆内 | C．在圆上 | D．不能确定 |
已知圆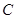
与直线
都相切，圆心在直线
上，则圆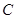的方程为（ ）
A． | B． |
C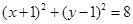． | D． |
已知圆
与直线
都相切，圆心在直线
上，则圆的方（ ）
A． | B． |
C． | D． |
圆
与圆
的位置关系为（ ）
| A．内切 | B．相交 | C．外切 | D．相离 |
圆C1: 
与圆C2:
的位置关系是（ ）
| A．外离 | B．外切 | C．内切 | D．相交 |
与圆
交于M,N两点，且M,N关于直线
对称，动点P(a，b)在不等式组
表示的平面区域内部及边界上运动，则
取值范围是（ ）
