题目内容
设圆
的圆心为C，A(1,0)是圆内一定点，Q为圆周上任一点．线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为( )．
A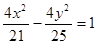． | B． |
C． | D． |
D
解析试题分析：∵．线段AQ的垂直平分线与CQ的连线交于点M，∴
，∴点M的轨迹为以点A、C为焦点的椭圆，故2a=5，2c=2，∴
，∴
，故点M的轨迹方程为，选D。
考点：本题主要考查了轨迹方程的求法。
点评：求动点轨迹问题时，动点的几何特征与平面几何中的定理及有关平面几何知识有着直接或间接的联系，且利用平面几何的知识得到包含已知量和动点坐标的等式，化简后就可以得到动点的轨迹方程，这种求轨迹方程的方法称作几何法
练习册系列答案
相关题目
已知圆的方程为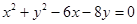
.设该圆过点H（3，5）的两条弦分别为AC和BD，且
.则四边形ABCD的面积最大值为（ ）
A． | B． | C．49 | D．50 |
圆
与圆
的位置关系为（ ）
| A．内切 | B．相交 | C．外切 | D．相离 |
圆C1: 
与圆C2:
的位置关系是（ ）
| A．外离 | B．外切 | C．内切 | D．相交 |
若直线3x＋y＋a＝0过圆x2＋y2＋2x－4y＝0的圆心，则a的值为( )
| A．－1 | B．1 | C．3 | D．－3 |
：
与圆
：
位置关系是（ ）已知圆
,
过点
的直线,则（ ）
A．与 相交 | B．与相切 |
| C．与相离 | D．以上三个选项均有可能 |
与圆
交于M,N两点，且M,N关于直线
对称，动点P(a，b)在不等式组
表示的平面区域内部及边界上运动，则
取值范围是（ ）
任意的实数k，直线
与圆
的位置关系一定是 （ ）
| A．相离 | B．相切 | C．相交但直线不过圆心 | D．相交且直线过圆心 |