题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1 , BC的中点. 
(1)证明:DE∥平面A1B1C;
(2)若AB=2,∠BAC=60°,求直线DE与平面ABB1A1所成角的正弦值.
【答案】
(1)证明:取AC的中点F,连接DF,EF,∵E是BC的中点,∴EF∥AB,
∵ABC﹣A1B1C1是三棱柱,∴AB∥A1B1,∴EF∥A1B1,
∴EF∥平面A1B1C,
∵D是AA1的中点,∴DF∥A1C,∴DF∥平面A1B1C,
又EF∩DE=E,
∴平面DEF∥平面A1B1C,∴DE∥平面A1B1C
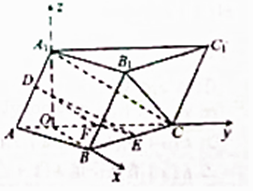
(2)解:过点A1作A1O⊥AC,垂足为O,连接OB,
∵侧面ACC1A⊥底面ABC,∴A1O⊥平面ABC,∴A1O⊥OB,A1O⊥OC,
∵∠A1AC=60°,AA1=2,∴OA=1, ![]() ,
,
∵AB=2,∠OAB=60°,由余弦定理得,OB2=OA2+AB2﹣2OAABcos∠BAC=3,
∴ ![]() ,∠AOB=90°,∴OB⊥AC,
,∠AOB=90°,∴OB⊥AC,
分别以OB,OC,OA1为x轴,y轴,z轴,建立如图的空间直角坐标系O﹣xyz,
由题设可得A(0,﹣1,0),C(0,3,0), ![]() ,
, ![]() ,
, 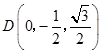 ,
, 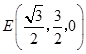 ,
,
设 ![]() 是平面ABB1A1的一个法向量,
是平面ABB1A1的一个法向量,
则 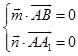 ,∴
,∴ 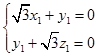 ,
,
令z1=1,∴ ![]() ,
,
∵ 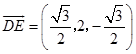 ,
,
∴ ![]() =
= 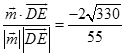 ,
,
∴直线DE与平面ABB1A1所成角的正弦值为 ![]() .
.
【解析】(1)取AC的中点F,连接DF,EF,由E是BC的中点,利用三角形中位线定理可得EF∥AB,再利用三棱柱的性质、线面平行的判定定理可得:EF∥平面A1B1C,DF∥平面A1B1C,可得平面DEF∥平面A1B1C,即可证明DE∥平面A1B1C.(2)过点A1作A1O⊥AC,垂足为O,连接OB,利用面面垂直的性质定理可得:A1O⊥平面ABC,A1O⊥OB,A1O⊥OC.利用余弦定理得,OB2=OA2+AB2﹣2OAABcos∠BAC=3,可得 ![]() ,进而得到OB⊥AC.分别以OB,OC,OA1为x轴,y轴,z轴,建立如图的空间直角坐标系O﹣xyz,利用平面法向量的夹角公式即可得出.
,进而得到OB⊥AC.分别以OB,OC,OA1为x轴,y轴,z轴,建立如图的空间直角坐标系O﹣xyz,利用平面法向量的夹角公式即可得出.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则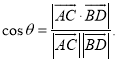 才能正确解答此题.
才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案


