Question

【题目】求以圆C1：x2＋y2－12x－2y－13＝0和圆C2：x2＋y2＋12x＋16y－25＝0的公共弦为直径的圆C的方程.

Answer 1

【答案】x2＋y2－4x＋4y－17＝0

【解析】试题分析：解法一：先两圆方程相减，得到公共弦方程，再联立直线和圆的方程求出公共点坐标，进而求出圆的半径和圆心，写出圆的方程即可；解法二：先两圆方程相减，得到公共弦方程，再利用圆系方程进行求解.

试题解析：解法一：联立两圆方程，

相减得公共弦所在直线方程为4x＋3y－2＝0.

再由，

联立得两圆交点坐标(－1,2)、(5，－6)．

∵所求圆以公共弦为直径，

∴圆心C是公共弦的中点(2，－2)，半径为，

∴圆C的方程为(x－2)2＋(y＋2)2＝25.

解法二：由解法一可知公共弦所在直线方程为4x＋3y－2＝0.设所求圆的方程为x2＋y2－12x－2y－13＋λ(x2＋y2＋12x＋16y－25)＝0(λ为参数)．

可求得圆心．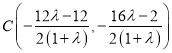

∵圆心C在公共弦所在直线上，

∴，

解得λ＝.

∴圆C的方程为x2＋y2－4x＋4y－17＝0.