题目内容
设数列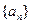 的前
的前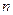 项和为
项和为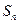 ,且方程
,且方程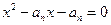 有一根为
有一根为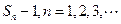 。
。
(Ⅰ)求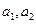 ;(Ⅱ)猜想数列
;(Ⅱ)猜想数列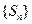 的通项公式,并给出严格的证明。
的通项公式,并给出严格的证明。
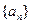 的前
的前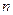 项和为
项和为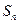 ,且方程
,且方程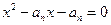 有一根为
有一根为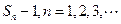 。
。(Ⅰ)求
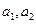 ;(Ⅱ)猜想数列
;(Ⅱ)猜想数列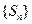 的通项公式,并给出严格的证明。
的通项公式,并给出严格的证明。解:(Ⅰ) 即
即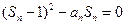
令
 解得
解得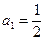
令
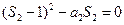 解得
解得
(Ⅱ)解法一:
化简得

令 解得
解得
所以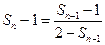
令
所以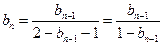 化简得
化简得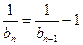
而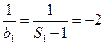
所以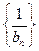 是以-2为首项,-1为公差的等差数列
是以-2为首项,-1为公差的等差数列
所以 得
得
解法二:猜想 ,下面用数学归纳法证明:
,下面用数学归纳法证明:
(1) 当 时,
时,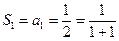 ,所以当
,所以当 时猜想成立
时猜想成立
(2) 假设当 时,猜想成立
时,猜想成立
即
那么当 时,
时,

所以当 时猜想成立。
时猜想成立。
综合(1)、(2)可得对于任意的正整数猜想都成立。
 即
即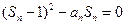
令

 解得
解得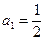
令

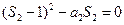 解得
解得
(Ⅱ)解法一:

化简得


令
 解得
解得
所以
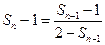
令

所以
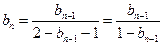 化简得
化简得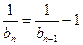
而
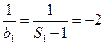
所以
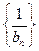 是以-2为首项,-1为公差的等差数列
是以-2为首项,-1为公差的等差数列所以
 得
得
解法二:猜想
 ,下面用数学归纳法证明:
,下面用数学归纳法证明:(1) 当
 时,
时,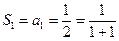 ,所以当
,所以当 时猜想成立
时猜想成立(2) 假设当
 时,猜想成立
时,猜想成立即

那么当
 时,
时,
所以当
 时猜想成立。
时猜想成立。综合(1)、(2)可得对于任意的正整数猜想都成立。
略

练习册系列答案
相关题目
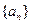 满足
满足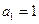 ,
,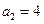 ,
,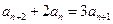
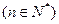 ,设
,设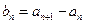 .
.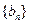 、
、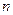 项和
项和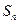 ,求使得
,求使得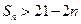 成立的最小整数
成立的最小整数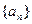 的前
的前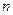 项和为
项和为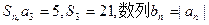 ,求数列
,求数列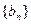 的前
的前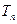
 ,本年度旅游收入为400万元,由于该项建设对旅游的促进作用,预计今后的旅游业收入每年会比上年平均增加
,本年度旅游收入为400万元,由于该项建设对旅游的促进作用,预计今后的旅游业收入每年会比上年平均增加 .
. 年(本年度为第一年)的投入为
年(本年度为第一年)的投入为 万元,旅游业收入为
万元,旅游业收入为 万元,写出
万元,写出
 ,猜想
,猜想 的表达式为 ( )A.
的表达式为 ( )A. ;
; 
 ; C.
; C. ; D.
; D. .
.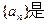 等比数列,其中
等比数列,其中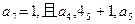 成等差数列.
成等差数列.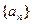 的通项公式;
的通项公式;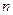 项和记为
项和记为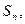 证明:
证明: 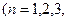 …).
…).
 的首项
的首项 为
为 (
( ),且
),且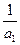 ,
, ,
, 成等比数列(Ⅰ)求数列
成等比数列(Ⅰ)求数列 ,试比较
,试比较 与
与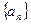 中,
中,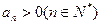 且
且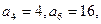 则数列
则数列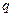 是 ( )
是 ( )
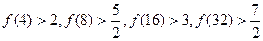 ,则推测当
,则推测当 时有
时有