题目内容
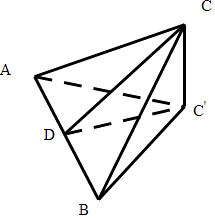
【题目】一边长为2的正三角形ABC的两个顶点A、B在平面α上,另一个顶点C在平面α上的射影为C',则三棱锥A﹣BC'C的体积的最大值为 .
【答案】![]()
【解析】解:设AB的中点为D,连接CD,C′D,
∵△ABC是边长为2的等边三角形,∴AB⊥CD,CD= ![]() .
.
∵CC′⊥α,ABα,
∴CC′⊥AB,又CD∩CC′=C,
∴AB⊥平面CDC′,
∴∠CDC′为平面ABC与平面α所成的角,
设∠CDC′=θ,则CC′=CDsinθ= ![]() sinθ,C′D=
sinθ,C′D= ![]() cosθ,
cosθ,
∴S△CDC′= ![]() =
= ![]() sinθcosθ=
sinθcosθ= ![]() sin2θ,
sin2θ,
∴VC﹣ABC′= ![]() =
= ![]() =
= ![]() sin2θ,
sin2θ,
∴当2θ= ![]() 即
即 ![]() 时,V取得最大值
时,V取得最大值 ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
相关题目