题目内容
设函数f（x）=（x2+2x-2）ex，求f（x）的极大值．
考点：利用导数研究函数的极值
专题：计算题,导数的综合应用
分析：求导f′（x）=（x2+4x）ex，从而确定函数的单调性及极大值．
解答：
解：f（x）=（x2+2x-2）ex，
f′（x）=（x2+4x）ex，
则当x＜-4或x＞0时，f′（x）＞0，
当-4＜x＜0时，f′（x）＜0；
故f（x）在x=-4时有极大值，
f（x）的极大值为f（-4）=
．
f′（x）=（x2+4x）ex，
则当x＜-4或x＞0时，f′（x）＞0，
当-4＜x＜0时，f′（x）＜0；
故f（x）在x=-4时有极大值，
f（x）的极大值为f（-4）=
| 6 |
| e4 |
点评：本题考查了导数在求极值时的应用，注意判断单调性，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若a=ln2，b=ln3，c=lg0.1，则a，b，c的大小顺序是（ ）
| A、a＞b＞c |
| B、c＞b＞a |
| C、b＞a＞c |
| D、b＞c＞a |
y=x2-3x+2在∈[
，3]上的最小值与最大值分别为（ ）
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
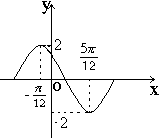函数y=Acos（ωx+φ）在一个周期内的图象如下，此函数的解析式为（ ）A、y=2cos（2x+
| ||||
B、y=2cos（2x-
| ||||
C、y=2cos（
| ||||
D、y=2cos（2x+
|
曲线y2=|x|+1的部分图象是（ ）
A、 |
B、 |
C、 |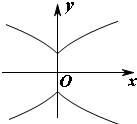
D、 |