题目内容

如图，已知二面角A-PC-B为直二面角，且PA⊥平面ABC，求证：△ABC为直角三角形．
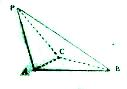
考点：直线与平面垂直的性质
专题：证明题,空间位置关系与距离
分析：过A作AD⊥PC，可证AD⊥BC，又证PA⊥BC，从而有BC⊥面PAC，可得BC⊥AC，即可证明△ABC为直角三角形．
解答：
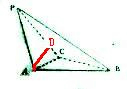
证明：过A作AD⊥PC，
∵A-PC-B为直二面角
∴AD⊥面PCB
∴AD⊥BC
又PA⊥平面ABC
∴PA⊥BC
∴BC⊥面PAC
∴BC⊥AC
∴△ABC为直角三角形，得证．
点评：本题主要考察了平面与平面垂直的性质，作辅助线AD是关键，属于基本知识的考查．
练习册系列答案
相关题目
若函数f（x）=log2x，则f（2）的值是（　　）
A、2B、0C、1D、4
已知A（1，0）、B（-2，0），动点M满足∠MBA=2∠MAB（∠MAB≠0）．
（1）求动点M的轨迹E的方程；
（2）若直线l：y=k（x+7），且轨迹E上存在不同的两点C、D关于直线l对称，求直线l斜率k的取值范围．
设函数f（x）=（x2+2x-2）ex，求f（x）的极大值．
设椭圆
x2
4
+y2=1的左、右焦点分别为F1，F2，M为椭圆上异于长轴端点的一点，∠F1MF2=2θ，△MF1F2的内心为I，
则|MI|cosθ=
 
．
设f（x）=-x3+ax2+bx+c（a＞0），在x=1处取得极大值，
（1）若曲线y=f（x）在点（
1
3
，f（
1
3
））处切线的斜率为
4
3
，求a，b；
（2）若曲线y=f（x）存在斜率为
4
3
的切线．求a的取值范围；
（3）在（2）的条件下，是否存在实数a，使得对?x∈（-∞，0]，都有f（x）≥c．
函数f（x）=
x+
1
x
，x∈[-2，-1]
x-
1
x
，x∈[
1
2
，2]
，则f（x）的值域为
 
．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞0，b＞0）的离心率为
1
2
，直线x=2被椭圆E截得的弦长为6，设F的椭圆E的右焦点，A为椭圆E的左顶点．
（1）求椭圆E的方程；
（2）求过点A、F，并且与椭圆的E右准线l相切的圆的方程；
（3）若M为椭圆E的右准线l上一点，连结AM交椭圆于点P，求
PM
AP
的取值范围．
直线l：y=m（m为实常数）与曲线E：y=|lnx|的两个交点A、B的横坐标分别为x1、x2，且x1＜x2，曲线E在点A、B处的切线PA、PB与y轴分别交于点M、N．有下面5个结论：
①|
MN
|=2；
②三角形PAB可能为等腰三角形；
③若直线l与y轴的交点为Q，则|PQ|=1；
④若点P到直线l的距离为d，则d的取值范围为（0，1）；
⑤当x1是函数g（x）=x2+lnx的零点时，|
AO
|（0为坐标原点）取得最小值．
其中正确结论有
 
．（写出所有正确结论的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网