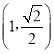题目内容
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
【答案】(1)x2+(y﹣1)2=1(y≠0).(2)![]() .
.
【解析】
(1)设出![]() 的极坐标,然后由题意得出极坐标方程,最后转化为直角坐标方程为
的极坐标,然后由题意得出极坐标方程,最后转化为直角坐标方程为![]() ;
;
(2)利用(1)中的结论,设出点的极坐标,然后结合面积公式得到面积的三角函数,结合三角函数的性质可得![]() 面积的最大值为
面积的最大值为![]() .
.
解:(1)设P的极坐标为(ρ,θ)(ρ>0),M的极坐标为(ρ0,θ)(ρ0>0).
由题设知|PO|=ρ,![]() .
.
由![]() 4,
4,
得![]() ,
,
所以C2的极坐标方程ρ=2sinθ(ρ>0),
因此C2的直角坐标方程为x2+(y﹣1)2=1(y≠0).
(2)依题意:![]() ,|OB|=ρ2=2sinα.
,|OB|=ρ2=2sinα.
于是△OAB面积:S![]() .
.
当![]() 时,S取得最大值
时,S取得最大值![]() .
.
所以△OAB面积的最大值为![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩共分五组,得到如下的频率分布表:
名学生的笔试成绩,按成绩共分五组,得到如下的频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
(1)请写出频率分布表中![]() 、
、![]() 、
、![]() 的值,若同组中的每个数据用该组区间的中间值代替,请估计全体考生的平均成绩;
的值,若同组中的每个数据用该组区间的中间值代替,请估计全体考生的平均成绩;
(2)为了能选出最优秀的学生,高校决定在笔试成绩高的第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名考生进入第二轮面试,求第
名考生进入第二轮面试,求第![]() 、
、![]() 、
、![]() 组中每组各抽取多少名考生进入第二轮的面试;
组中每组各抽取多少名考生进入第二轮的面试;
(3)在(2)的前提下,学校要求每个学生需从![]() 、
、![]() 两个问题中任选一题作为面试题目,求第三组和第五组中恰好有
两个问题中任选一题作为面试题目,求第三组和第五组中恰好有![]() 个学生选到问题
个学生选到问题![]() 的概率.
的概率.