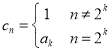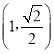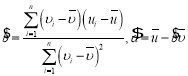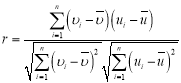题目内容
【题目】已知函数![]() .
.
(Ⅰ)求证:当![]() 时,
时,![]() 的图象位于直线
的图象位于直线![]() 上方;
上方;
(Ⅱ)设函数![]() ,若曲线
,若曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且在点
轴平行,且在点![]() 处的切线与直线
处的切线与直线![]() 平行(
平行(![]() 为坐标原点),求证:
为坐标原点),求证: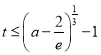 .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.
【解析】
(Ⅰ)转化为当![]() 时,
时,![]() 恒成立,令
恒成立,令![]() ,求得
,求得![]() 和
和![]() ,结合函数的单调性,求得
,结合函数的单调性,求得![]() ,进入得到
,进入得到![]() ,即可得到结论.
,即可得到结论.
(Ⅱ)设![]() ,由
,由![]() ,解得
,解得![]() ,得到
,得到![]() ,所以
,所以![]() ,进而得到要证
,进而得到要证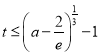 ,转化为
,转化为![]() ,构造新函数
,构造新函数![]() ,求得函数的单调性与最值,即可求解.
,求得函数的单调性与最值,即可求解.
(Ⅰ)由题意,当![]() 时,
时,![]() 的图象位于直线
的图象位于直线![]() 上方,
上方,
即证当![]() 时,
时,![]() 恒成立,
恒成立,
令![]() ,可得
,可得![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
所以当![]() 时,
时,![]() 的图象始终在直线
的图象始终在直线![]() 上方.
上方.
(Ⅱ)因为![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
要证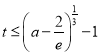 ,
,
即证![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
下面证明![]() .令
.令![]() ,∴
,∴![]() ,
,
所以当![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,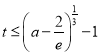 .
.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】针对某新型病毒,某科研机构已研发出甲乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有![]() 的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占
的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占![]() .
.
产生抗体 | 未产生抗体 | 合计 | |
甲 | |||
乙 | |||
合计 |
(1)根据题中数据,完成列联表;
(2)根据(1)中的列联表,判断能否有![]() 的把握认为甲乙两种疫苗的效果有差异.
的把握认为甲乙两种疫苗的效果有差异.
参考公式: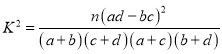 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩共分五组,得到如下的频率分布表:
名学生的笔试成绩,按成绩共分五组,得到如下的频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
(1)请写出频率分布表中![]() 、
、![]() 、
、![]() 的值,若同组中的每个数据用该组区间的中间值代替,请估计全体考生的平均成绩;
的值,若同组中的每个数据用该组区间的中间值代替,请估计全体考生的平均成绩;
(2)为了能选出最优秀的学生,高校决定在笔试成绩高的第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名考生进入第二轮面试,求第
名考生进入第二轮面试,求第![]() 、
、![]() 、
、![]() 组中每组各抽取多少名考生进入第二轮的面试;
组中每组各抽取多少名考生进入第二轮的面试;
(3)在(2)的前提下,学校要求每个学生需从![]() 、
、![]() 两个问题中任选一题作为面试题目,求第三组和第五组中恰好有
两个问题中任选一题作为面试题目,求第三组和第五组中恰好有![]() 个学生选到问题
个学生选到问题![]() 的概率.
的概率.