题目内容
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 的周长为12.
的周长为12.
(1)求点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)已知点![]() ,是否存在过点
,是否存在过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
【答案】(1)![]() ;(2)不存在,答案见解析.
;(2)不存在,答案见解析.
【解析】
(1)依题意根据椭圆的定义可知点![]() 的轨迹为椭圆,(除去与x轴的交点),
的轨迹为椭圆,(除去与x轴的交点),
设方程为![]() ,由
,由![]() ,
,![]() ,求出
,求出![]() 即可得到椭圆方程;
即可得到椭圆方程;
(2显然直线![]() 的斜率不存在时,直线与椭圆无交点;当直线
的斜率不存在时,直线与椭圆无交点;当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,联立直线与椭圆方程,消元,由
,联立直线与椭圆方程,消元,由![]() 求出
求出![]() 的取值范围,设点
的取值范围,设点![]() ,
,![]() 的中点
的中点![]() ,列出韦达定理,表示出
,列出韦达定理,表示出![]() ,由又
,由又![]() ,得到
,得到![]() ,得到方程判断方程的解即可;
,得到方程判断方程的解即可;
解:(1)由题意可得![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() 的周长为12,
的周长为12,
∴![]() ,
,
∴点P的轨迹是椭圆(除去与x轴的交点),
设方程为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴点![]() 的轨迹C的方程为
的轨迹C的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,直线与椭圆无交点;
的斜率不存在时,直线与椭圆无交点;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的斜率为k,
的斜率为k,
则![]() ,
,
联立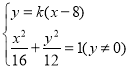 ,
,
得![]() ,
,
由![]() ,
,
解得![]() ,且
,且![]() .
.
设点![]() ,
,![]() 的中点
的中点![]()
∵![]() ,∴
,∴![]()
![]()
又∵![]() ,∴
,∴![]() ,
,
∵![]()
∴![]() ,此方程无解.
,此方程无解.
综上所述,不存在直线![]() 使得
使得![]() .
.

练习册系列答案
相关题目