题目内容
14.已知函数f(x)=|2x-1|,f(a)>f(b)>f(c),则以下情况不可能发生的是( )| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
分析 当x≤0时,函数f(x)=1-2x,f(x)递减;当x≥0时,函数f(x)=2x-1,f(x)递增,结合f(a)>f(b)>f(c),分析出a,b,c,0可能大小关系,可得答案.
解答 解:∵函数f(x)=|2x-1|,
当x≤0时,函数f(x)=1-2x,f(x)递减;
当x≥0时,函数f(x)=2x-1,f(x)递增,
若f(a)>f(b)>f(c),
则可能为:a<b<c≤0,
也可能为:a<c≤0<b且a<-b<c≤0,
也可能为:b<c≤0<a且-a<b<c≤0,
只有b<a<c不可能.
故选D.
点评 本题考查的知识点是指数单调性,函数图象的对折变换,难度不大,属于基础题.

练习册系列答案
相关题目
9.已知集合A={x||x-$\frac{1}{2}$|≤$\frac{3}{2}$},B={x|y=lg(4x-x2)},则A∩B等于( )
| A. | (0,2] | B. | [-1,0) | C. | [2,4) | D. | [1,4) |
6.如图所示,当输入的实数x∈[2,30]时,执行如图所示的程序框图,则输出的x不小于111的概率是( )


| A. | $\frac{8}{13}$ | B. | $\frac{17}{28}$ | C. | $\frac{2}{3}$ | D. | $\frac{18}{29}$ |
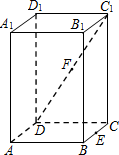 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: