题目内容
【题目】已知U=R且A={x|a2x2-5ax-6<0},B{x||x-2|≥1}.
(1)若a=1,求(UA)![]() B;
B;
(2)求不等式a2x2-5ax-6<0(a∈R)的解集.
【答案】(1){x|x≤-1或x≥6};(2)a=0时,不等式的解集为R;a>0时,不等式的解集为(-![]() ,
,![]() );a<0时,不等式的解集为(
);a<0时,不等式的解集为(![]() ,-
,-![]() ).
).
【解析】
(1)解不等式求出集合![]() ,
,![]() ,再由集合运算法则计算.
,再由集合运算法则计算.
(2)分类讨论,![]() ,
,![]() 时,方程
时,方程![]() 两根为
两根为![]() 和
和![]() ,按它们的大小分类得解集.
,按它们的大小分类得解集.
(1)a=1时,A={x|x2-5x-6<0}={x|-1<x<6},B={x||x-2|≥1}={x|x≤1或x≥3};
∴UA={x|x≤-1或x≥6},
则(UA)![]() B={x|x≤-1或x≥6};
B={x|x≤-1或x≥6};
(2)a=0时,不等式化为-6<0,解集为R;
当a≠0时,不等式化为(ax+1)(ax-6)<0,即(x+![]() )(x-
)(x-![]() )<0;
)<0;
若a>0,则-![]() <
<![]() ,不等式的解集为(-
,不等式的解集为(-![]() ,
,![]() );
);
若a<0,则-![]() >
>![]() ,不等式的解集为(
,不等式的解集为(![]() ,-
,-![]() );
);
综上知,a=0时,不等式的解集为R;
a>0时,不等式的解集为(-![]() ,
,![]() );
);
a<0时,不等式的解集为(![]() ,-
,-![]() ).
).

【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的![]() 城市和交通拥堵严重的
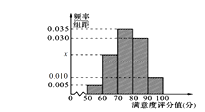
城市和交通拥堵严重的![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小(不要求计算具体值,给出结论即可);
(2)若得分不低于85分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此列联表,并据此样本分析是否有![]() 的把握认为城市拥堵与认可共享单车有关;
的把握认为城市拥堵与认可共享单车有关;
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)若此样本中的![]() 城市和
城市和![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自![]() 城市的概率是多少?
城市的概率是多少?
(参考公式: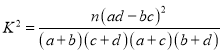 )
)
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |