题目内容
【题目】如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥平面ABCD，点E、F分别是AB和PC的中点．
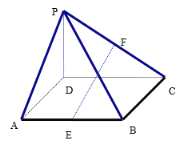
(1)求证：AB⊥平面PAD；
(2)求证：EF//平面PAD．
【答案】（1）证明见解析（2）证明见解析
【解析】
（1）证明PA⊥AB，AD⊥AB，证得AB⊥平面PAD．
（2）取CD的中点G，由FG是三角形CPD的中位线，可得 FG∥PD，再由矩形的性质得 EG∥AD，证明平面EFG∥平面PAD，从而证得EF∥平面PAD．
（1）∵侧棱PA垂直于底面，∴PA⊥AB．又底面ABCD是矩形，∴AD⊥AB，
这样，AB垂直于平面PAD内的两条相交直线，∴AB⊥平面PAD．
（2）取CD的中点G，∵E、F分别是AB、PC的中点，∴FG是三角形CPD的中位线，
∴FG∥PD，FG∥面PAD．∵底面ABCD是矩形，∴EG∥AD，EG∥平面PAD．
故平面EFG∥平面PAD，∴EF∥平面PAD．
练习册系列答案
相关题目
【题目】随着共享单车的蓬勃发展，越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况，某共享单车公司对某区域不同年龄的骑乘者进行了调查，得到数据如下：
年龄 | 15 | 25 | 35 | 45 | 55 | 65 |
骑乘人数 | 95 | 80 | 65 | 40 | 35 | 15 |
（1）求
关于
的线性回归方程，并估计年龄为40岁人群的骑乘人数；
（2）为了回馈广大骑乘者，该公司在五一当天通过
向每位骑乘者的前两次骑乘分别随机派送一张面额为1元，或2元，或3元的骑行券.已知骑行一次获得1元券，2元券，3元券的概率分别是
，
，
，且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车，记该骑乘者当天获得的骑行券面额之和为
，求的分布列和数学期望.
参考公式：
，
.
参考数据：
，
.
