题目内容
【题目】在复平面内，给出以下四个说法：
①实轴上的点表示的数均为实数；
②虚轴上的点表示的数均为纯虚数；
③互为共轭复数的两个复数的实部相等，虚部互为相反数；
④已知复数
满足
，则在复平面内所对应的点位于第四象限.
其中说法正确的个数为（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据复数的几何意义可判断出命题①②的正误，根据共轭复数的概念判断命题③的正误，利用复数的除法求出复数
，结合复数的几何意义可判断出命题④的正误.
对于命题①，由复数的几何意义知，实轴上的点表示的数均为实数，命题①正确；
对于命题②，原点在虚轴上，原点代表的数为零，不是纯虚数，命题②错误；
对于命题③，互为共轭复数的两个复数的实部相等，虚部互为相反数，命题③正确；
对于命题④，由
，得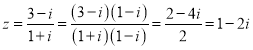
，所以，复数在复平面内所对应的点在第四象限，命题④正确.
因此，正确的命题为①③④.
故选：C.
练习册系列答案
高中必刷题系列答案
相关题目
