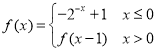题目内容
【题目】已知函数f(x)=lnx![]() ,a∈R.
,a∈R.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若x>1时,f(x)>0,求a的取值范围.
【答案】(1) x+8y﹣1=0,(2) (﹣∞,2].
【解析】
(1)由x=2是函数f(x)的极值点,可得,f′(2)=0,代入可求a,然后结合导数的几何意义即可求解,
(2)先对函数求导,然后结合导数与单调性的关系对a进行分类讨论即可求解.
(1)∵f′(x)![]() ,
,
由x=2是函数f(x)的极值点,可得,f′(2)=0,
∴a![]() ,
,
∴y=f(x)在点(1,f(1))处的切线斜率k=f′(1)![]() ,
,
又f(1)=0
故y=f(x)在点(1,f(1))处的切线方程y![]() 即x+8y﹣1=0,
即x+8y﹣1=0,
(2)若a≤2,x>1时,f′(x)![]() 0,
0,
∴f(x)在(1,+∞)上单调递增,f(x)>f(1)=0,符合题意,
若a>2,方程x2+(2﹣2a)+1=0的△=4a2﹣8a>0,
∴x2+(2﹣2a)+1=0有两个不等的根,设两根分别为x1,x2,且x1<x2,
∵x1+x2=2a﹣2,x1x2=1,
∴0<x1<1<x2,<0,f′(x)<0,f(x)单调递减,
当x∈(1,x2)时,x2+(2﹣2a)+1<0,f′(x)<0,f(x)单调递减,
f(x)<f(1)=0,不符合题意,
综上可得,a的范围(﹣∞,2].

练习册系列答案
相关题目