题目内容
【题目】已知关于x的不等式|x﹣a|＜b的解集为{x|2＜x＜4}．
（Ⅰ）求实数a，b的值；
（Ⅱ）设实数x，y，z 满足 
+ 
+ 
=1，求x，y，z的最大值和最小值．
【答案】解：（Ⅰ）由|x﹣a|＜b解得{x|a﹣b＜x＜a+b}，结合不等式|x﹣a|＜b的解集为{x|2＜x＜4}， 可得a﹣b=2且a+b=4，解得a=3，b=1．
（Ⅱ）依题意有 
+ 
+ 
=1，由柯西不等式知
[42+ 
+22][ + + ]≥ 
，
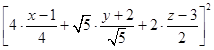即25×1≥（x+y+z﹣2）2 ， 解得﹣3≤x+y+z≤7，
当且仅当x= 
，y=﹣1，z= 
时，x+y+z=7；
当且仅当x=﹣ 
，y=﹣3，z= 时，x+y+z=﹣3；
所以，x+y+z的最大值为7，最小值为﹣3
【解析】（Ⅰ）由|x﹣a|＜b解得{x|a﹣b＜x＜a+b}，结合不等式|x﹣a|＜b的解集为{x|2＜x＜4}，可得a﹣b=2且a+b=4，由此求得a、b的值．（Ⅱ）由条件利用柯西不等式求得x，y，z的最大值和最小值．
【考点精析】掌握绝对值不等式的解法是解答本题的根本，需要知道含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．
练习册系列答案
阅读快车系列答案
相关题目
