题目内容
【题目】已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出f(x)的周期、振幅、初相、对称轴;
(3)此函数图象由y=sinx的图象怎样变换得到?(注:y轴上每一竖格长为1)

【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析.
【解析】试题分析:
(1)由题意结合五点法列表,据此绘制函数图象即可;
(2)结合函数的解析式可得函数的周期为![]() ,振幅为3,初相为
,振幅为3,初相为![]() ,对称轴方程为:
,对称轴方程为:![]() .
.
(3)结合三角函数的变换性质可知变换过程如下:由y=sinx在[0,2π]上的图象向左平移![]() 个单位,把横坐标伸长为原来的2倍,把纵坐标伸长为原来的3倍,向上平移3个单位,即可得到
个单位,把横坐标伸长为原来的2倍,把纵坐标伸长为原来的3倍,向上平移3个单位,即可得到![]() 的图象.
的图象.
试题解析:
(1)令![]() 取0,
取0,![]() ,π,
,π,![]() ,2π,列表如下:
,2π,列表如下:
| 0 |
| π |
| 2π |
x |
|
|
|
|
|
| 3 | 6 | 3 | 0 | 3 |
在一个周期内的闭区间上的图象如下图所示:
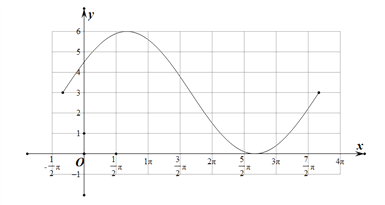
(2)∵函数![]() 中,A=3,B=3,ω=
中,A=3,B=3,ω=![]() ,φ=
,φ=![]() .
.
∴函数f(x)的周期T=4π,振幅为3,初相为![]() ,
,
对称轴满足:![]() ,
,
据此可得对称轴方程为:![]() .
.
(3)此函数图象可由y=sinx在[0,2π]上的图象经过如下变换得到:
①向左平移![]() 个单位,得到y=sin(x+
个单位,得到y=sin(x+![]() )的图象;
)的图象;
②再保持纵坐标不变,把横坐标伸长为原来的2倍得到y=![]() 的图象;
的图象;
③再保持横坐标不变,把纵坐标伸长为原来的3倍得到y=![]() 的图象;
的图象;
④再向上平移3个单位,得到![]() 的图象.
的图象.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目