题目内容
若直线ax-by+2=0（a＞0，b＞0）经过圆x2+y2+2x-2y=7的圆心，则ab的最大值是（ ）
| A．1 | B．2 | C．4 | D．
|
由圆x2+y2+2x-2y=7得（x+1）2+（y-1）2=9，∴圆心P（-1，1）．
∵直线ax-by+2=0（a＞0，b＞0）经过圆心P（-1，1），∴-a-b+2=0，得到a+b=2．
∵a＞0，b＞0，∴2=a+b≥2
，∴ab≤1．当且仅当a=b=1时取等号．
故ab的最大值为1．
故选A．
∵直线ax-by+2=0（a＞0，b＞0）经过圆心P（-1，1），∴-a-b+2=0，得到a+b=2．
∵a＞0，b＞0，∴2=a+b≥2
| ab |
故ab的最大值为1．
故选A．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
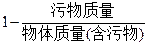)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
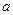(1≤a≤3).设用
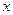单位质量的水初次清洗后的清洁度是
(
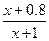),用
质量的水第二次清洗后的清洁度是
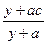,其中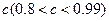
是该物体初次清洗后的清洁度.
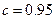时方案乙的用水量,并比较哪一种方案用水量较少;