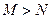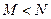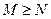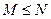题目内容
下列函数中,最小值为4的函数是( )
A.y=lgx+
| B.y=sinx+
| ||||
| C.y=ax+4a-x (a>0,a≠1) | D.y=x+
|
由于当x>0时,lgx可正可负,则y=lgx+
的值可为负数,故A错误
令t=sinx,则t∈(0,1]y=sinx+
=t+
在(0,1]上单调递减,则t=1时,函数有最小值5,故B错误
由于ax>0,则y=ax+
≥2
=4,当且仅当ax=
即ax=2时取等号,即函数的最小值为4
x>1可得x-1>0,y=x+
=x-1+
+1≥2
+1=5,故函数的最小值5
故选C
| 4 |
| lgx |
令t=sinx,则t∈(0,1]y=sinx+
| 4 |
| sinx |
| 4 |
| t |
由于ax>0,则y=ax+
| 4 |
| ax |
ax•
|
| 4 |
| ax |
x>1可得x-1>0,y=x+
| 4 |
| x-1 |
| 4 |
| x-1 |
(x-1)•
|
故选C

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
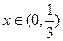 ,则函数
,则函数 的最大值为 .
的最大值为 .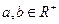 ,且
,且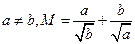 ,
, 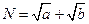 ,则
,则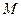 与
与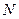 的大小关系是
的大小关系是