题目内容
【题目】已知数列{an}满足![]() .
.
(1)求a1,a2,a3的值;
(2)对任意正整数n,an小数点后第一位数字是多少?请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.见解析
;(2)a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.见解析
【解析】
(1)因为数列{an}满足![]() ,令n=1,n=2,n=3,分别求解.
,令n=1,n=2,n=3,分别求解.
(2)根据a1,a2小数点后第一位数字均为5,a3小数点后第一位数字为6,猜想对任意正整数n(n≥3),均有0.6<an<0.7,根据![]() ,所以对任意正整数n(n≥3),有an≥a3>0.6,只要证明:对任意正整数n(n≥3),有
,所以对任意正整数n(n≥3),有an≥a3>0.6,只要证明:对任意正整数n(n≥3),有![]() 即可.采用数学归纳法证明.
即可.采用数学归纳法证明.
(1)a1![]() ,a2
,a2![]() ;a3
;a3![]() ,
,
可得![]() ,
,![]() ,
,![]() ;
;
(2)a1,a2小数点后第一位数字均为5,a3小数点后第一位数字为6,
下证:对任意正整数n(n≥3),均有0.6<an<0.7,
注意到![]() ,
,
故对任意正整数n(n≥3),有an≥a3>0.6,
下用数学归纳法证明:对任意正整数n(n≥3),有![]()
①当n=3时,有![]() ,命题成立;
,命题成立;
②假设当n=k(k∈N*,k≥3)时,命题成立,即![]()
则当n=k+1时,![]()
∵![]()
∴![]() ∴
∴![]()
∴n=k+1时,命题也成立;
综合①②,任意正整数n(n≥3),![]() .
.
由此,对正整数n(n≥3),0.6<an<0.7,此时an小数点后第一位数字均为6.
所以a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到下图的率分布直方图.(同一组数据用该区间的中点值作代表)
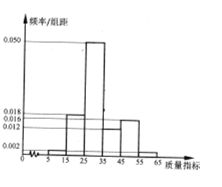
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名联客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.