��Ŀ����
����Ŀ��ij�ֲ�Ʒ��������������ָ��ֵ����������������ָ��ֵ���ֵȼ������
����ָ��ֵm | 25��m��35 | 15��m��25��35��m��45 | 0��m��15��45��m��65 |
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
ij��ҵ�����������ֲ�Ʒ�г�ȡ100����Ʒ��Ϊ���������������ָ��ֵ���õ���ͼ���ʷֲ�ֱ��ͼ����ͬһ�������ø�������е�ֵ��������
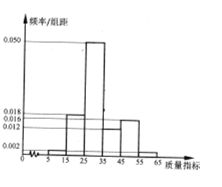
��1������ҵΪ��߲�Ʒ��������չ���������������������ٳ�����⣬��Ʒ����Ʒ��Y��������Y��H��10��15��100�����������������������������ֲ�Ʒ��������Ʒ������һ������Ʒ��ռȫ����Ʒ�ٷֱȣ��ϻǰ��߶��ٸ��ٷֵ㣿
��2������ҵÿ��һ��Ʒ�ۼ�180Ԫ��ÿ������Ʒ�ۼ�150Ԫ��ÿ������Ʒ�ۼ�120Ԫ���������е�Ƶ�ʴ�����Ӧ���ʣ�����һ�������������������Ʒ������֧���ķ���ΪX����λ��Ԫ������X�ķֲ��м���ѧ������
���𰸡���1��5���ٷֵ㣮��2����������![]() ��
��
��������
��1�����ݳ����������ݣ����������һ��Ʒ�Ͷ���Ʒ�ļ������õ�����������ռ�������ٸ��ݻ���Ʒ����Ʒ��Y��������Y��H��10��15��100���õ�һ������Ʒ�ĺϸ��ʣ����������Ƚϼ���.
��2��������Ʒ�������壬����ҵ�����ȡһ����ƷΪһ��Ʒ�ĸ���Ϊ![]() ������Ʒ�ĸ���Ϊ
������Ʒ�ĸ���Ϊ![]() ������Ʒ�ĸ���Ϊ
������Ʒ�ĸ���Ϊ![]() ������ȷ�������X�����п���ȡֵΪ240��270��300��330��360���ֱ������Ӧ���ʣ�д���ֲ�����������.
������ȷ�������X�����п���ȡֵΪ240��270��300��330��360���ֱ������Ӧ���ʣ�д���ֲ�����������.
��1�����ݳ�����������֪��������һ��Ʒ�Ͷ���Ʒ���У���0.5+0.18+0.12����100��80������
����������ռ����Ϊ80%��
����Ʒ����Ʒ��Y��������Y��H��10��15��100����
����100����Ʒ������ƷΪ15����һ������Ʒ��Ϊ100��15��85�������ϸ���Ϊ85%��
����һ������Ʒ��������5���ٷֵ㣮
��2������Ʒ��������֪������ҵ�����ȡһ����ƷΪһ��Ʒ�ĸ���Ϊ![]() ������Ʒ�ĸ���Ϊ
������Ʒ�ĸ���Ϊ![]() ������Ʒ�ĸ���Ϊ
������Ʒ�ĸ���Ϊ![]() ��
��
�������X�����п���ȡֵΪ240��270��300��330��360��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����X�ķֲ���Ϊ��
X | 240 | 270 | 300 | 330 | 360 |
P��X�� |
|
|
|
|
|
X����ѧ����![]() ��
��

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д�