题目内容
【题目】已知函数
是
上的增函数.当实数
取最大值时，若存在点
，使得过点的直线与曲线
围成两个封闭图形，且这两个封闭图形的面积总相等，则点的坐标为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】分析：求出函数的导数，利用导数研究函数的单调性，求出m的最大值，结合过点Q的直线与曲线
围成两个封闭图形，且这两个封闭图形的面积总相等，判断函数的对称性进行求解即可.
详解：由
得
，
是
上的增函数，
在上恒成立，即：
在上恒成立.
设
， 
， 
，
设
，，
，
函数在单调递增，
.
即
，
，
又
， 
.
m的最大值为3.
故得
.
将函数的图象向上平移3个长度单位，所得图象相应的函数解析式为
.
由于
，
为奇函数，
故的图象关于原点对称，
由此即得函数的图象关于
成中心对称.
这表明存在点，使得过点
的直线与曲线围成两个封闭图形，且这两个封闭图形的面积总相等.
故选：C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图（1））和女生身高情况的频率分布直方图（图（2））．已知图（1）中身高在170～175cm的男生人数有16人．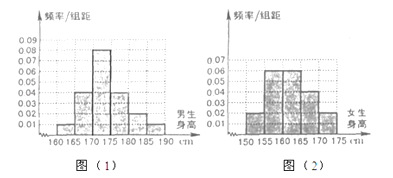
（Ⅰ）试问在抽取的学生中，男、女生各有多少人？
（Ⅱ）根据频率分布直方图，完成下列的2×2列联表，并判断能有多大（百分几）的把握认为“身高与性别有关”？
≥170cm | ＜170cm | 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
（Ⅲ）在上述80名学生中，从身高在170～175cm之间的学生中按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率．
参考公式：K2=
参考数据：
P（K2≥k0） | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
