Question

【题目】在直角坐标系xOy中，设倾斜角为α的直线： （t为参数）与曲线C： （θ为参数）相交于不同的两点A，B．
（1）若α= ，求线段AB的长度；
（2）若直线的斜率为 ，且有已知点P（2， ），求证：|PA||PB|=|OP|2 ．

Answer 1

【答案】
（1）

解：由曲线C： （θ为参数），可得C的普通方程是 =1．

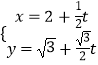当 时，直线方程为： （t为参数），

代入曲线C的普通方程，得13t2+56t+48=0，

则线段AB的长度为

（2）

证明：将直线l的参数方程代入曲线C的普通方程，

化为：（cos2α+4sin2α）t2+（8 sinα+4cosα）t+12=0，

∵ ，

而直线的斜率为 ，则 代入上式求得|PA||PB|=7．

又 ，

∴|PA||PB|=|OP|2

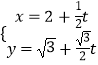【解析】（1）由曲线C： （θ为参数），利用平方关系可得C的普通方程．当 时，直线方程为： （t为参数），代入代入曲线C的普通方程，得13t2+56t+48=0，利用一元二次方程的根与系数的关系、弦长公式即可得出．（2）将直线l的参数方程代入曲线C的普通方程，化为：（cos2α+4sin2α）t2+（8 sinα+4cosα）t+12=0，利用根与系数的关系即可得出．