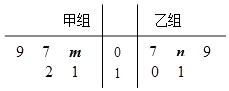
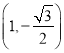题目内容
【题目】若sin2α= ![]() ,sin(β﹣α)=
,sin(β﹣α)= ![]() ,且α∈[
,且α∈[ ![]() ,π],β∈[π,
,π],β∈[π, ![]() ],则α+β的值是( )
],则α+β的值是( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
【答案】A
【解析】解:∵α∈[ ![]() ,π],β∈[π,
,π],β∈[π, ![]() ],∴2α∈[
],∴2α∈[ ![]() ,2π],
,2π],
又sin2α= ![]() >0,
>0,
∴2α∈[ ![]() ,π],cos2α=﹣
,π],cos2α=﹣ ![]() =﹣
=﹣ ![]() ;
;
又sin(β﹣α)= ![]() ,β﹣α∈[
,β﹣α∈[ ![]() ,π],
,π],
∴cos(β﹣α)=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴cos(α+β)=cos[2α+(β﹣α)]=cos2αcos(β﹣α)﹣sin2αsin(β﹣α)=﹣ ![]() ×(﹣
×(﹣ ![]() )﹣
)﹣ ![]() ×
× ![]() =
= ![]() .
.
又α∈[ ![]() ,
, ![]() ],β∈[π,
],β∈[π, ![]() ],
],
∴(α+β)∈[ ![]() ,2π],
,2π],
∴α+β= ![]() ,
,
故选:A.
【考点精析】通过灵活运用两角和与差的正弦公式和二倍角的正弦公式,掌握两角和与差的正弦公式:![]() ;二倍角的正弦公式:
;二倍角的正弦公式:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目