题目内容
【题目】记等差数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若 ![]() ,对任意
,对任意![]() ,均有
,均有![]() 是公差为
是公差为![]() 的等差数列,求使
的等差数列,求使![]() 为整数的正整数
为整数的正整数![]() 的取值集合;
的取值集合;
(3)记![]() ,求证:
,求证: ![]() .
.
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】【试题分析】(1)先设等差数列![]() 的公差为
的公差为![]() ,将
,将![]() ,进而得到当
,进而得到当![]() 时,
时, ![]() ,依据定义可知数列
,依据定义可知数列![]() 是等差数列;(2)依据题设条件“任意的
是等差数列;(2)依据题设条件“任意的![]() 都是公差为
都是公差为![]() ,的等差数列”求出
,的等差数列”求出![]() ,然后建立等式
,然后建立等式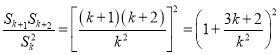 ,分析探求出
,分析探求出![]() 满足条件,当
满足条件,当![]() 时不满足,进而求出正整数
时不满足,进而求出正整数![]() 的取值集合为
的取值集合为![]() ;(3)先依据题设将问题转化为证明不等式
;(3)先依据题设将问题转化为证明不等式![]() 。证明时运用了做差比较的方法进行推证,进而证得
。证明时运用了做差比较的方法进行推证,进而证得![]()
![]() ,使得不等式或获证。
,使得不等式或获证。
解:(1)设等差数列![]() 的公差为
的公差为![]() ,则
,则![]() ,从而
,从而![]() ,所以当
,所以当![]() 时,
时, ![]() ,即数列
,即数列![]() 是等差数列.
是等差数列.
(2)因为的任意的![]() 都是公差为
都是公差为![]() ,的等差数列,所以
,的等差数列,所以![]() 是公差为
是公差为![]() ,的等差数列,又
,的等差数列,又![]() ,所以
,所以![]() ,所以
,所以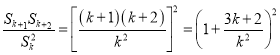 ,显然,
,显然, ![]() 满足条件,当
满足条件,当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() 不是整数,综上所述,正整数
不是整数,综上所述,正整数![]() 的取值集合为
的取值集合为![]() .
.
(3)设等差数列![]() 的公差为
的公差为![]() ,则
,则![]() ,所以
,所以![]() ,即数列
,即数列![]() 是公比大于
是公比大于![]() ,首项大于
,首项大于![]() 的等比数列,记公比为
的等比数列,记公比为![]() .以下证明:
.以下证明: ![]() ,其中
,其中![]() 为正整数,且
为正整数,且![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,因为
时,因为![]() 为减函数,
为减函数, ![]() ,所以
,所以![]() ,所以
,所以![]() ,综上,
,综上, ![]() ,其中
,其中![]()
![]()
![]() ,即
,即![]() .
.

 考前必练系列答案
考前必练系列答案【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
【题目】已知函数f(x)=x2+bx+c满足f(2﹣x)=f(2+x),f(0)>0,且f(m)=f(n)=0(m≠n),则log4m﹣ ![]() n的值是( )
n的值是( )
A.小于1
B.等于1
C.大于1
D.由b的符号确定
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于![]() 为合格品,小于
为合格品,小于![]() 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共![]() 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
芯片数量(件) |
|
|
|
|
|
已知生产一件芯片,若是合格品可盈利![]() 元,若是次品则亏损
元,若是次品则亏损![]() 元.
元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产![]() 件芯片所获得的利润不少于
件芯片所获得的利润不少于![]() 元的概率.
元的概率.
(Ⅱ)记![]() 为生产
为生产![]() 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量![]() 的分布列和数学期望
的分布列和数学期望