题目内容
【题目】已知函数
，
，
（1）若函数
的图象与函数
的图象相切，求
的值；
（2）设函数
，
. 若存在
，
，使
成立，求的取值范围.
【答案】（1）
，（2）
的取值范围为
【解析】
（1）设切点为
，由导数的几何意义可得
，
，然后即可解出答案
（2）首先利用导数求出
的单调区间，然后分
、
、
三种情况讨论，每种情况求出的最大值和最小值，然后解出不等式
即可.
（1）设切点为
因为
，
，函数
的图象与函数
的图象相切
所以，
解得
，
（2）
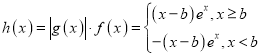
当
时，
，所以在
上为增函数
当
时，
因为
时，
，所以在
上为减函数
因为
时，
，所以在
上为增函数
①当时，在
上为增函数
所以
，
由得
，所以
②当时，
因为
时，，所以在
上为增函数
因为
时，，所以在
上为减函数
，
所以，
由得
因为，
，所以
③当时，同理可得在上为减函数，在上为增函数
所以
，
由得
，不成立
综上：的取值范围为
练习册系列答案
阅读快车系列答案
相关题目
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌，得到如下
列联表：
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
（1）从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本，现从这5名学生中随机选取3名做深度采访，求这3名学生中恰有2名挑同桌的概率；
（2）根据以上列联表，是否有
以上的把握认为“性别与在选择座位时是否挑同桌”有关？
下面的临界值表供参考：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（参考公式：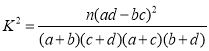
，其中
