题目内容
【题目】已知各项均不相等的等差数列{an}的前n项和为Sn,S10=45,且a3,a5,a9恰为等比数列{bn}的前三项,记![]() .
.
(1)分别求数列{an}、{bn}的通项公式;
(2)若m=17,求cn取得最小值时n的值;
(3)当c1为数列{cn}的最小项时, ![]() 有相应的可取值,我们把所有am的和记为A1;…;当ci为数列
有相应的可取值,我们把所有am的和记为A1;…;当ci为数列![]() 的最小项时,
的最小项时,![]() 有相应的可取值,我们把所有am的和记为Ai;…,令Tn= A1+ A2+…+An,求Tn.
有相应的可取值,我们把所有am的和记为Ai;…,令Tn= A1+ A2+…+An,求Tn.
【答案】(1)![]() ,
,![]() ;(2)0;(3)
;(2)0;(3)![]()
【解析】分析:(1)先利用等比中项和等差数列的通项公式、前![]() 项和公式得到关于首项和公差的方程组,进而得到等差数列的通项公式,再利用等比数列的前三项求出等比数列的通项公式;(2)化简
项和公式得到关于首项和公差的方程组,进而得到等差数列的通项公式,再利用等比数列的前三项求出等比数列的通项公式;(2)化简![]() ,得到关于
,得到关于![]() 的二次函数,利用函数的单调性进行求解;(3)化简
的二次函数,利用函数的单调性进行求解;(3)化简![]() ,得到关于
,得到关于![]() 的二次函数,利用换元思想,讨论二次函数的对称轴、单调性进行求解.
的二次函数,利用换元思想,讨论二次函数的对称轴、单调性进行求解.
详解:(1)由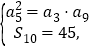
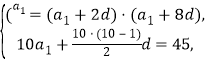
![]() ,
,
∴an=n1,
∴b1=a3=2,b2=a5=4,b3=a9=8,易得bn=2n.
(2) 若 m=17,则 cn=(2n16)( 2n+116)=2(2n12)232,
当n=3或n=4,cn取得最小值0.
(3) cn=(bnam) (bn+1am) =22n+13(m1)2n +(m1)2,
令2n =tn,则cn=f(tn)=2tn 23(m1)tn+(m1)2,根据二次函数的图象和性质,当c1取得最小值时,t1在抛物线对称轴tn =![]() 的左、右侧都有可能,但t2≤t3≤t4≤…都在对称轴的右侧,必有
的左、右侧都有可能,但t2≤t3≤t4≤…都在对称轴的右侧,必有
c2≤c3≤c4≤….而c1取得最小值,∴c1≤c2≤c3≤c4≤…,等价于c1≤c2.
由c1≤c2解得1≤m≤5,∴A1=a1+a2+…+a5=10,
同理,当ci(i==2,3, …)取得最小值时,只需![]()
![]()
解得![]() ,
,
∴![]() .
.
可得![]() .
.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案