题目内容
【题目】已知函数![]()
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)证明当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立;
恒成立;
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)令![]() ,求出函数的导数,得到函数的单调区间,求出函数的最大值,从而证出结论即可;
,求出函数的导数,得到函数的单调区间,求出函数的最大值,从而证出结论即可;
解析:
(1)![]() ,
,
由f'(x)<0,得2x2﹣x﹣1>0.又x>0,所以x>1,
所以f(x)的单调递减区间为(1,+∞),函数f(x)的单增区间为(0,1).
(2)令![]() ,
,
所以![]() ,
,
因为a≥2,所以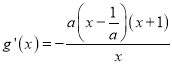 ,
,
令g'(x)=0,得![]() ,所以当
,所以当![]() ,当
,当![]() 时,g'(x)<0,
时,g'(x)<0,
因此函数g(x)在![]() 是增函数,在
是增函数,在![]() 是减函数,
是减函数,
故函数g(x)的最大值为![]() ,
,
令![]() ,因为
,因为![]() ,又因为h(a)在a∈(0,+∞)是减函数,
,又因为h(a)在a∈(0,+∞)是减函数,
所以当a≥2时,h(a)<0,即对于任意正数x总有g(x)<0,
所以关于x的不等式恒成立.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目