题目内容
7.定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)},仍是等比数列,则称f(x)为“等比函数”.现有定义在(-∞),0)∪(0,+∞)上的如下函数:①f(x)=3x,
②f(x)=$\frac{2}{x}$,
③f(x)=x3,
④f(x)=log2|x|,
则其中是“等比函数”的f(x)的序号为( )
| A. | ①②③④ | B. | ①④ | C. | ①②④ | D. | ②③ |
分析 不妨设等比数列{an}中,an=a1•qn-1,从而依次求$\frac{f({a}_{n+1})}{f({a}_{n})}$,从而判断是否是等比数列即可.
解答 解:不妨设等比数列{an}中,an=a1•qn-1,
①∵f(x)=3x,
∴$\frac{f({a}_{n+1})}{f({a}_{n})}$=$\frac{{3}^{{a}_{n+1}}}{{3}^{{a}_{n}}}$=$\frac{{3}^{{a}_{1}{q}^{n}}}{{3}^{{a}_{1}{q}^{n-1}}}$
=${3}^{{q}^{n}-{q}^{n-1}}$=${3}^{{q}^{n-1}(1-q)}$常数,
故当q≠1时,{f(an)}不是等比数列,
故f(x)=3x不是等比函数;
②∵f(x)=$\frac{2}{x}$,
∴$\frac{f({a}_{n+1})}{f({a}_{n})}$=$\frac{\frac{2}{{a}_{1}{q}^{n}}}{\frac{2}{{a}_{1}{q}^{n-1}}}$=$\frac{{a}_{1}{q}^{n-1}}{{a}_{1}{q}^{n}}$=$\frac{1}{q}$,
故{f(an)}是等比数列,
故f(x)=$\frac{2}{x}$是等比函数;
③∵f(x)=x3,
∴$\frac{f({a}_{n+1})}{f({a}_{n})}$=$\frac{({a}_{1}{q}^{n})^{3}}{({a}_{1}{q}^{n-1})^{3}}$═q3,
故{f(an)}是等比数列,
故f(x)=x3是等比函数;
④f(x)=log2|x|,
∴$\frac{f({a}_{n+1})}{f({a}_{n})}$=$\frac{lo{g}_{2}|{a}_{1}{q}^{n}|}{lo{g}_{2}|{a}_{1}{q}^{n-1}|}$=$\frac{lo{g}_{2}|{a}_{1}|+nlo{g}_{2}|q|}{lo{g}_{2}|{a}_{1}|+(n-1)lo{g}_{2}|q|}$,
故{f(an)}不是等比数列,
故f(x)=log2|x|不是等比函数.
故其中是“等比函数”的f(x)的序号②③,
故选:D.
点评 本题考查了等比数列的应用及等比函数的判断,同时考查了学生对新知识的接受与应用能力.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | m<1 | B. | m≤1 | C. | m>1 | D. | m<2 |
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5}{6}$π | D. | $\frac{π}{3}$ |
| A. | (-∞,0]∪[2,+∞) | B. | (-∞,0]∪(2,+∞) | C. | (-∞,0)∪[2,+∞) | D. | (-∞,0)∪(2,+∞) |
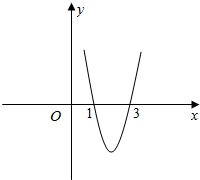 已知奇函数f(x)在(0,+∞)上的图象如图所示,则不等式$\frac{f(x)}{x-1}<0$的解集为( )
已知奇函数f(x)在(0,+∞)上的图象如图所示,则不等式$\frac{f(x)}{x-1}<0$的解集为( )| A. | (-3,-1)∪(0,1)∪(1,3) | B. | (-3,-1)∪(0,1)∪(3,+∞) | C. | (-∞,-3)∪(-1,0)∪(3,+∞) | D. | (-∞,-3)∪(-1,0)∪(0,1) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |