题目内容
7．
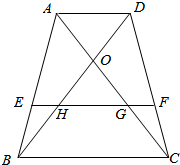已知，如图所示，在梯形ABCD中，AD∥BC∥EF，对角线DB与AC交于点O，与EF分别交于点H、G，求证：EH=GF．
分析 AD∥BC∥EF，利用平行线间线段成比例，得到HF=EG，即可得出结论．
解答 证明：∵AD∥BC∥EF，
∴由平行线间线段成比例，得到：HF：BC=DF：DC=AE：AB=EG：BC，
∴HF=EG，
∴EH=EG-HG=HF-HG=GF．
点评 本题考查平行线间线段成比例，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
15．正四棱锥P-ABCD内接于球，底面ABCD是和球心O在同一平面内，球的体积为$\frac{8\sqrt{2}π}{3}$，则正四棱锥P-ABCD的表面积为 （ ）
| A． | 4$\sqrt{3}$ | B． | 4+4$\sqrt{3}$ | C． | 4+4$\sqrt{2}$ | D． | 4+8$\sqrt{3}$ |
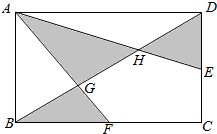如图：长方体ABCD中，AB=10厘米，BC=15厘米，E，F分别是所在边的中点，求阴影部分的面积．（提示：由于图中AD平行于BC，可知AD：BF=AG：CF=DG：BG）
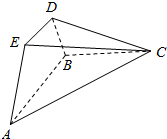已知△ABC为直角三角形，AB⊥BC，四边形ABDE为等腰梯形，DE∥AB，平面ABDE⊥平面ABC，AB=BC=2DE=2．
19．已知正方体、等边圆柱（轴截面是正方形）、球的体积相等，它们的表面积分别为S正、S柱、S球，则（ ）
| A． | S正＜S球＜S柱 | B． | S正＜S柱＜S球 | C． | S球＜S柱＜S正 | D． | S球＜S正＜S柱 |
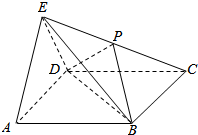如图，在四棱锥E-ABCD中，底面ABCD为正方形，侧面EAD是正三角形，平面EAD⊥平面ABCD为正方形，P为EC的中点．