题目内容
16.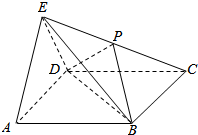 如图,在四棱锥E-ABCD中,底面ABCD为正方形,侧面EAD是正三角形,平面EAD⊥平面ABCD为正方形,P为EC的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,侧面EAD是正三角形,平面EAD⊥平面ABCD为正方形,P为EC的中点.(1)求证:EA∥平面PBD;
(2)若正方形ABCD的边长为2,求三棱锥E-PBD的体积及点P到平面EBD的距离.
分析 (1)连结AC,与BD交于点O,连接OP,则O是AC的中点,OP∥AE,即可证明EA∥平面PBD;
(2)三棱锥E-PBD的体积=三棱锥E-BCD的体积-三棱锥P-BDC的体积,利用体积公式,可求点P到平面EBD的距离.
解答  (1)证明:如图,连结AC,与BD交于点O,连接OP,则O是AC的中点,
(1)证明:如图,连结AC,与BD交于点O,连接OP,则O是AC的中点,
又P为EC的中点,∴OP∥AE.
又∵AE?平面PBD,OP?PBD,
∴EA∥平面PBD;
(2)解:三棱锥E-PBD的体积=三棱锥E-BCD的体积-三棱锥P-BDC的体积
=$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}$-$\frac{1}{3}×\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$.
△EBD中,ED=2,BD=2$\sqrt{2}$,EB=2$\sqrt{2}$,
∴S△EBD=$\frac{1}{2}×2×\sqrt{8-1}$=$\sqrt{7}$,
设P到平面EBD的距离为h,则$\frac{1}{3}×\sqrt{7}×h$=$\frac{\sqrt{3}}{3}$,
∴h=$\frac{\sqrt{21}}{7}$.
点评 本题考查线面平行的判定,考查三棱锥的体积公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.设P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)上一点,F1(-c,0),F2(c,0)(c>0)为左、右焦点,△PF1F2周长为6c,面积为$\frac{2\sqrt{3}}{3}$a2,则双曲线的离心率是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
6.等比数列{an}中,a2=2,a5=$\frac{1}{4}$,则公比q=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
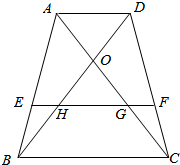 已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.
已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.