题目内容
19.已知正方体、等边圆柱(轴截面是正方形)、球的体积相等,它们的表面积分别为S正、S柱、S球,则( )| A. | S正<S球<S柱 | B. | S正<S柱<S球 | C. | S球<S柱<S正 | D. | S球<S正<S柱 |
分析 利用正方体、等边圆柱(轴截面是正方形)、球的体积、表面积公式,即可得出结论.
解答 解:正方体的棱长为a,体积V=a3,S正=6a2=6$\root{3}{{V}^{2}}$
等边圆柱(轴截面是正方形)的高为2h,体积V=π•h2•2h=2πh3,S柱=6πh2=3$\root{3}{2π{V}^{2}}$
球的半径为R,体积V=$\frac{4}{3}π{R}^{3}$,S球=4πR2=$\root{3}{36π{V}^{2}}$
∴S球<S柱<S正,
故选:C.
点评 本题考查正方体、等边圆柱(轴截面是正方形)、球的体积、表面积公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
11.设P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)上一点,F1(-c,0),F2(c,0)(c>0)为左、右焦点,△PF1F2周长为6c,面积为$\frac{2\sqrt{3}}{3}$a2,则双曲线的离心率是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
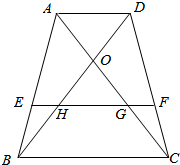 已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.
已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.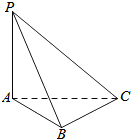 如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.
如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.