题目内容
2.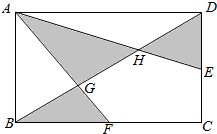 如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)
如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)
分析 因为BF与AD平行,并且等于AD的$\frac{1}{2}$,所以BG:GD=BE:AD=1:2,则BG:BD=1:3,同样的方法可以得出:DH:BD=1:3,所以BG=DH=$\frac{1}{3}$BD,所以BG=GH=HD,所以△ABG与△AGH的面积相等,△ABG的面积+△BGE的面积=△AGH的面积+△BGE的面积,△AGH的面积+△BGE的面积=△ABE的面积,利用三角形的面积公式即可求解;又因△DEH的DE边上的高=$\frac{1}{3}$BC,从而可以求其面积,据此即可求解.
解答 解:因为BF与AD平行,并且等于AD的$\frac{1}{2}$,
所以BG:GD=BF:AD=1:2,则BG:BD=1:3,
同样的方法可以得出:DH:BD=1:3,
所以BG=DH=$\frac{1}{3}$BD,所以BG=GH=HD,
所以△ABG与△AGH的面积相等,
△ABG的面积+△BGF的面积=△AGH的面积+△BGF的面积,
△AGH的面积+△BGF的面积=△ABF的面积=$\frac{1}{2}$×10×$\frac{15}{2}$=$\frac{75}{2}$(平方厘米);
又因△DEH的DE边上的高=$\frac{1}{3}$×15=5(厘米),
所以△DEH面积=$\frac{1}{2}$×5×5=$\frac{25}{2}$(平方厘米);
即阴影部分面积=$\frac{75}{2}$+$\frac{25}{2}$=50(平方厘米).
答:阴影部分的面积是50平方厘米.
点评 解答此题的主要依据是:相似三角形的面积比等于对应边的比.

练习册系列答案
相关题目
11.设P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)上一点,F1(-c,0),F2(c,0)(c>0)为左、右焦点,△PF1F2周长为6c,面积为$\frac{2\sqrt{3}}{3}$a2,则双曲线的离心率是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
 如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).
如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).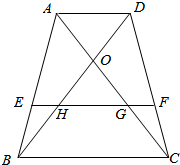 已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.
已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.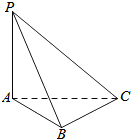 如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.
如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.