题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2ex,x<0}\\{{e}^{x},x≥0}\end{array}\right.$,其中e为自然对数的底数,若关于x的方程f(x)-a|x|=0(a∈R)有三个不同的实数根,则函数y=f(x)-a的零点个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由分段函数知需要讨论,当x≥0时,可得a=$\frac{{e}^{x}}{x}$,x>0;令g(x)=$\frac{{e}^{x}}{x}$,从而求导g′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$;从而判断函数的单调性及零点的个数;当x<0时,方程f(x)-a|x|=0可化为-x(x+2e-a)=0,从而确定a的取值范围;再按分段函数讨论即可.
解答 解:①当x≥0时,方程f(x)-a|x|=0可化为ex-ax=0,
故a=$\frac{{e}^{x}}{x}$,x>0;
令g(x)=$\frac{{e}^{x}}{x}$,g′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$;
故g(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
且g(1)=e;
故当a=e时,方程f(x)-a|x|=0在x≥0时有一个解,
当a<e时,方程f(x)-a|x|=0在x≥0时没有解,
当a>e时,方程f(x)-a|x|=0在x≥0时有两个解;
②当x<0时,方程f(x)-a|x|=0可化为-x(x+2e-a)=0,
故当a<2e时,方程f(x)-a|x|=0在x<0时有一个解,
当a≥2e时,方程f(x)-a|x|=0在x<0时没有解;
综上所述,若关于x的方程f(x)-a|x|=0(a∈R)有三个不同的实数根,
则e<a<2e;
当x<0时,令f(x)-a=-x2-2ex-a=0,
可化为x2+2ex+a=0,
由判别式△=4e2-4a>0,及根与系数的关系知,
方程有两个不同的负根;
当x≥0时,令f(x)-a=ex-a=0,
故x=lna;
故函数y=f(x)-a的零点个数为3;
故选:C.
点评 本题考查了导数的综合应用及分段函数的应用,同时考查了根与系数的关系应用.

| A. | ${C}_{4}^{3}$ | B. | ${P}_{4}^{3}$ | C. | ${4}_{\;}^{3}$ | D. | 34 |
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
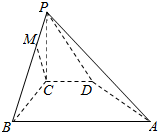 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证:
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证: 如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).
如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).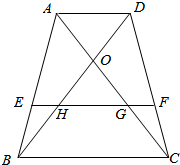 已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.
已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.