题目内容
17.已知函数f(x)=log2(4x+1)+kx,(k∈R)是偶函数,则k的值为-1.分析 根据偶函数的定义f(-x)=f(x),列出方程,利用对数的运算法则,求出k的值.
解答 解:∵函数f(x)=log2(4x+1)+kx,(k∈R)是偶函数,
∴f(-x)=f(x),
即log2(4-x+1)+k(-x)=log2(4x+1)+kx,
∴log2(4-x+1)-log2(4x+1)=2kx,
化简得-2x=2kx,
即(2k+2)x=0;
∴2k+2=0,
解得k=-1.
故答案为:-1.
点评 本题考查了对数函数的性质与应用问题,也考查了偶函数的定义与应用问题,是基础题目.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.等比数列{an}中,a2=2,a5=$\frac{1}{4}$,则公比q=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
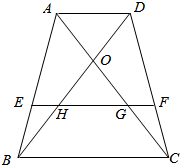 已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.
已知,如图所示,在梯形ABCD中,AD∥BC∥EF,对角线DB与AC交于点O,与EF分别交于点H、G,求证:EH=GF.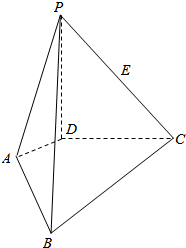 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.