题目内容
已知椭圆G: .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.
(1)求椭圆G的焦点坐标和离心率;
(2)将 表示为m的函数,并求
表示为m的函数,并求 的最大值.
的最大值.
 .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.(1)求椭圆G的焦点坐标和离心率;
(2)将
 表示为m的函数,并求
表示为m的函数,并求 的最大值.
的最大值.(1)
(2)2

(2)2
(1)由已知得,a=2,b=1,所以 .
.
所以椭圆G的焦点坐标为(- ,0),(
,0),( ,0),离心率为
,0),离心率为 .
.
(2)由题意知, .
.
当m=1时,切线l的方程为x=1,点A,B的坐标分别为 ,
, ,
,
此时 .
.
当m=-1时,同理可得 .
.
当 时,设切线l的方程为
时,设切线l的方程为 .
.
由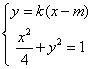 得
得 .
.
设A,B两点的坐标分别为 ,则
,则
 ,
, .
.
又由l与圆 相切,得
相切,得 ,即
,即 .
.
所以
 .
.
由于当 时,
时, ,
,
当 时,
时, ,
,
且当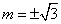 时,
时, ,所以
,所以 的最大值为2.
的最大值为2.
 .
.所以椭圆G的焦点坐标为(-
 ,0),(
,0),( ,0),离心率为
,0),离心率为 .
.(2)由题意知,
 .
.当m=1时,切线l的方程为x=1,点A,B的坐标分别为
 ,
, ,
,此时
 .
.当m=-1时,同理可得
 .
.当
 时,设切线l的方程为
时,设切线l的方程为 .
.由
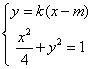 得
得 .
.设A,B两点的坐标分别为
 ,则
,则 ,
, .
.又由l与圆
 相切,得
相切,得 ,即
,即 .
.所以

 .
.由于当
 时,
时, ,
,当
 时,
时, ,
,且当
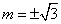 时,
时, ,所以
,所以 的最大值为2.
的最大值为2.
练习册系列答案
相关题目
 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 ;设
;设 为曲线
为曲线 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 两个不同的点.
两个不同的点. 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由; 的面积为
的面积为 ,
, 的面积为
的面积为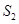 ,令
,令 ,求
,求 的最大值.
的最大值. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,则双曲线
,则双曲线 x
x  x
x 过点
过点 和点
和点 .
. 的方程;
的方程; 的直线
的直线 与椭圆
与椭圆 两点,且
两点,且 ,求直线
,求直线 的左、右焦点,A、B是以O(O
的左、右焦点,A、B是以O(O B.
B. C.
C. D.
D.
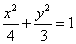 的左焦点为
的左焦点为 ,直线
,直线 与椭圆相交于点
与椭圆相交于点 、
、 ,当△FAB的周长最大时,
,当△FAB的周长最大时, 的面积是____________.
的面积是____________.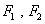 ,若曲线r上存在点P满足
,若曲线r上存在点P满足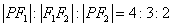 ,则曲线r的离心率等于( )
,则曲线r的离心率等于( ) 或
或
 或2
或2 的长轴在
的长轴在 轴上,焦距为
轴上,焦距为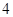 ,则
,则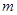 等于 ( )
等于 ( )



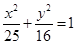 的长轴的端点、焦点,则双曲线C的方程为_______.
的长轴的端点、焦点,则双曲线C的方程为_______.