题目内容
17.若函数f(x)=2|sinx|+sinx,(x∈[0,2π])的图象与直线y=k有且仅有四个不同的交点,则k的取值范围是(0,1).分析 画出函数f(x)=2|sinx|+sinx=$\left\{\begin{array}{l}{3sinx,x∈[0,π)}\\{-sinx∈[π,2π]}\end{array}\right.$,(x∈[0,2π])以及直线y=k 的图象,数形结合可得k的取值范围.
解答 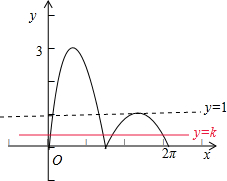 解:画出函数f(x)=2|sinx|+sinx=$\left\{\begin{array}{l}{3sinx,x∈[0,π)}\\{-sinx∈[π,2π]}\end{array}\right.$,(x∈[0,2π])以及直线y=k 的图象,
解:画出函数f(x)=2|sinx|+sinx=$\left\{\begin{array}{l}{3sinx,x∈[0,π)}\\{-sinx∈[π,2π]}\end{array}\right.$,(x∈[0,2π])以及直线y=k 的图象,
由f(x)的图象与直线y=k有且仅有四个不同的交点,可得0<k<1,
故答案为:(0,1).
点评 本题主要考查正弦函数的图象,体现了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
8.若实数x,y满足$\left\{\begin{array}{l}{x-2y+2<0}\\{x>0}\\{y<2}\end{array}\right.$,则$\frac{y}{x-1}$的取值范围为( )
| A. | (-∞,-1)∪(2,+∞) | B. | (-∞,-1)∪(0,2) | C. | (-1,0)∪(0,2) | D. | (-1,2) |
5.若不等式ax2+bx-1<0的解集为{x|-1<x<2},则a+b=( )
| A. | 6 | B. | 4 | C. | 2 | D. | 0 |
12.已知下列不等式①x2-4x+3<0;②x2-6x+8<0;③2x2-9x+a<0,且使不等式①②成立的x也满足③,则实数a的取值范围是( )
| A. | a≥$\frac{9}{4}$ | B. | a≤10 | C. | a≤9 | D. | a≥-4 |