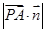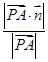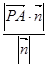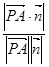题目内容
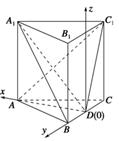
如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.

(1)求证:A1B∥平面ADC1;
(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.
(1)见解析(2)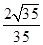
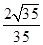
(1)证明:因为三棱柱ABC-A1B1C1是直三棱柱,所以四边形A1ACC1是矩形.连接A1C交AC1于O,则O是A1C的中点,又D是BC的中点,所以在△ADC1中,OD∥A1B,因为A1B?平面ADC1,OD?平面ADC1,所以A1B∥平面ADC1.
(2)解:因为△ABC是等边三角形,D是BC的中点,所以AD⊥BC.以D为原点,建立如图所示空间坐标系D-xyz.由已知AB=BB1=2,得D(0,0,0),A(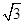 ,0,0),A1(
,0,0),A1(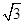 ,0,2),C1(0,-1,2).
,0,2),C1(0,-1,2).
则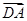 =(
=(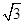 ,0,0),
,0,0), =(0,-1,2),设平面AC1D的法向量为n=(x,y,z),由
=(0,-1,2),设平面AC1D的法向量为n=(x,y,z),由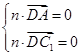 得
得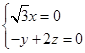
取z=1,则x=0,y=2,
∴n=(0,2,1),又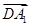 =(
=(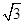 ,0,2),∴cos〈
,0,2),∴cos〈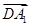 ,n〉=
,n〉=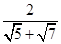 =
=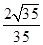 ,设A1D与平面ADC1所成角为θ,
,设A1D与平面ADC1所成角为θ,
则sin θ=|cos〈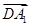 ,n〉|=
,n〉|=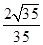 ,
,
故A1D与平面ADC1所成角的正弦值为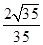 .
.
(2)解:因为△ABC是等边三角形,D是BC的中点,所以AD⊥BC.以D为原点,建立如图所示空间坐标系D-xyz.由已知AB=BB1=2,得D(0,0,0),A(
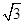 ,0,0),A1(
,0,0),A1(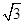 ,0,2),C1(0,-1,2).
,0,2),C1(0,-1,2).
则
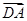 =(
=(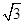 ,0,0),
,0,0), =(0,-1,2),设平面AC1D的法向量为n=(x,y,z),由
=(0,-1,2),设平面AC1D的法向量为n=(x,y,z),由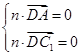 得
得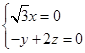
取z=1,则x=0,y=2,
∴n=(0,2,1),又
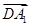 =(
=(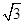 ,0,2),∴cos〈
,0,2),∴cos〈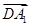 ,n〉=
,n〉=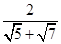 =
=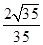 ,设A1D与平面ADC1所成角为θ,
,设A1D与平面ADC1所成角为θ,则sin θ=|cos〈
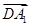 ,n〉|=
,n〉|=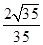 ,
,故A1D与平面ADC1所成角的正弦值为
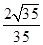 .
.
练习册系列答案
相关题目
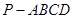 中,
中,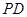
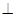 底面
底面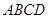 ,且底面
,且底面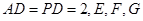 分别为
分别为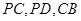 的中点.
的中点.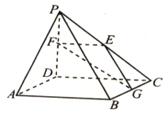
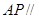 平面
平面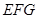 ;
;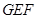 和平面
和平面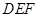 的夹角.
的夹角.  是边长为
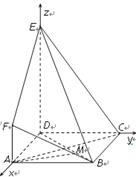
是边长为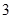 的正方形,
的正方形,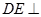 平面
平面 ,
,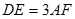 ,
,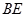 与平面
与平面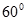 .
.
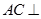 平面
平面 ;
;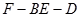 的余弦值;
的余弦值;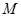 是线段
是线段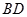 上一个动点,试确定点
上一个动点,试确定点 平面
平面 ,并证明你的结论.
,并证明你的结论. .
.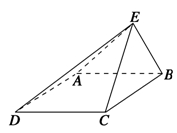
 的所有棱长都为4,D为的
的所有棱长都为4,D为的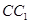 中点.
中点.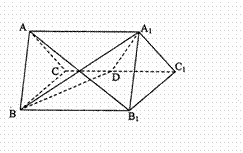
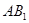 ⊥平面
⊥平面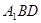 ;
;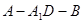 余弦值.
余弦值. |=
|= |
| |.
|.
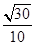
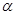 外一点,A为平面
外一点,A为平面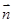 为平面
为平面