题目内容
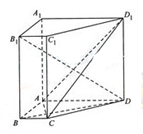
正三棱柱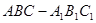 的所有棱长都为4,D为的
的所有棱长都为4,D为的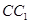 中点.
中点.
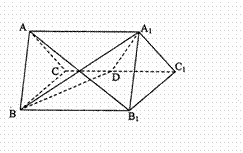
(1)求证: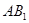 ⊥平面
⊥平面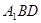 ;
;
(2)求二面角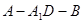 余弦值.
余弦值.
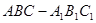 的所有棱长都为4,D为的
的所有棱长都为4,D为的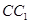 中点.
中点.
(1)求证:
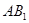 ⊥平面
⊥平面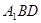 ;
;(2)求二面角
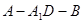 余弦值.
余弦值.(1)详见解析;(2)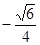 .
.
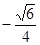 .
.试题分析:(1)先根据题意找到BC中点O,证明
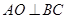 ,
,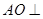 平面
平面 ,从而以O为原点构造出空间直角坐标系.在写出平面
,从而以O为原点构造出空间直角坐标系.在写出平面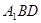 中相关向量坐标以及
中相关向量坐标以及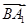 的坐标,由向量的数量积为0证明线线垂直,从而得到
的坐标,由向量的数量积为0证明线线垂直,从而得到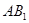 ⊥平面
⊥平面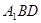 ;(2)先求出平面
;(2)先求出平面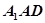 的法向量,又由上问可知平面
的法向量,又由上问可知平面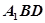 的法向量即
的法向量即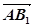 ,再通过向量的夹角公式得到这两个法向量的夹角余弦值,经观察可知即为二面角
,再通过向量的夹角公式得到这两个法向量的夹角余弦值,经观察可知即为二面角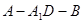 余弦值.从而得到本题的解.
余弦值.从而得到本题的解.试题解析:(1)取BC中点O,连AO,
∵
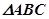 为正三角形, ∴
为正三角形, ∴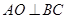 ,
, ∵在正三棱柱
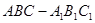 中,平面ABC
中,平面ABC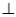 平面
平面 ,∴
,∴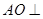 平面
平面 ,
, 取
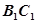 中点为
中点为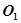 ,以O为原点,
,以O为原点,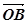 ,
,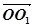 ,
,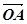 的方向为
的方向为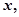
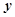 ,
,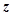 轴的正方向,建立空间直角坐标系,
轴的正方向,建立空间直角坐标系, 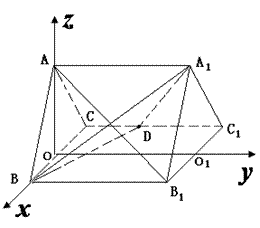
则
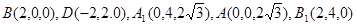 .
.∴
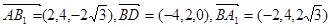 ,
, ∵
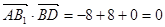 ,
,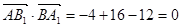 .
. ∴
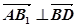 ,
,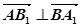 ,∴
,∴ 面
面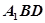
(2)设平面
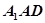 的法向量为
的法向量为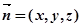 ,
,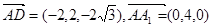 .
.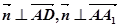 ,∴
,∴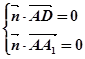 ,∴
,∴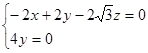 ,
,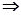
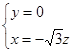 ,令
,令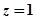 ,得
,得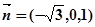 为平面
为平面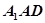 的一个法向量,由(1)知
的一个法向量,由(1)知 面
面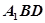 ,
, ∴
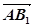 为平面
为平面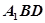 的法向量,
的法向量, ,
,经检验易知二面角
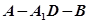 的余弦值为
的余弦值为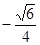 .
.
练习册系列答案
相关题目

 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,
, 底面
底面 ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
 平面
平面 ;
; 与
与 所成角的大小;
所成角的大小; 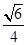 .
.
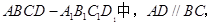
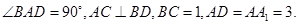
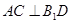 ;
;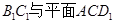 所成角的正弦值。
所成角的正弦值。 为正三角形,
为正三角形, ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在
 平面PBD;
平面PBD; 时,求二面角
时,求二面角 的余弦值。
的余弦值。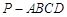 中
中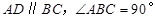 ,
,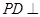 平面
平面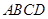 ,
,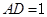 ,
,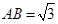 ,
,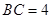 .
.
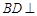
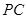 ;
;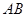 与平面
与平面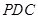 所成的角;
所成的角;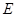 在棱
在棱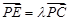 ,若
,若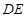 ∥平面
∥平面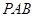 ,求
,求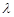 的值.
的值.