题目内容
如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=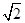 .
.
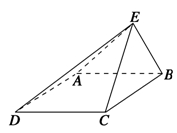
(1)求证:平面EAB⊥平面ABCD;
(2)求直线AE与平面CDE所成角的正弦值.
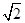 .
.
(1)求证:平面EAB⊥平面ABCD;
(2)求直线AE与平面CDE所成角的正弦值.
(1)见解析(2)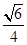
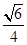
(1)证明 取AB的中点O,连接EO,CO,∵AE=EB=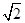 ,AB=2,∴△AEB为等腰直角三角形,∴EO⊥AB,EO=1,又∵AB=BC,∠ABC=60°.
,AB=2,∴△AEB为等腰直角三角形,∴EO⊥AB,EO=1,又∵AB=BC,∠ABC=60°.
∴△ACB是等边三角形,∴CO=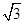 ,又EC=2,∴EC2=EO2+CO2,∴EO⊥CO.
,又EC=2,∴EC2=EO2+CO2,∴EO⊥CO.
又∵CO∩AB=O,∴EO⊥平面ABCD,又EO?平面EAB,∴平面EAB⊥平面ABCD.
(2)解 以AB中点O为坐标原点,分别以OC,OB,OE所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
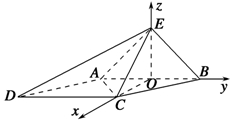
则A(0,-1,0),C(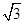 ,0,0),D
,0,0),D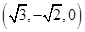 ,E(0,0,1).
,E(0,0,1).
∴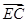 =(
=(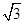 ,0,-1),
,0,-1),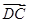 =(0,2,0),
=(0,2,0),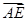 =(0,1,1).
=(0,1,1).
设平面CDE的法向量n=(x,y,z),
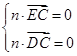
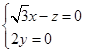 令z=1,解得
令z=1,解得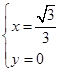
∴平面CDE的一个法向量n=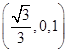 ,设直线AE与平面CDE所成角为θ.
,设直线AE与平面CDE所成角为θ.
∴sin θ=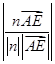 =
=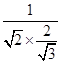 =
=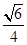 .
.
∴直线AE与平面CDE所成角的正弦值是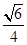 .
.
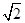 ,AB=2,∴△AEB为等腰直角三角形,∴EO⊥AB,EO=1,又∵AB=BC,∠ABC=60°.
,AB=2,∴△AEB为等腰直角三角形,∴EO⊥AB,EO=1,又∵AB=BC,∠ABC=60°.∴△ACB是等边三角形,∴CO=
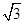 ,又EC=2,∴EC2=EO2+CO2,∴EO⊥CO.
,又EC=2,∴EC2=EO2+CO2,∴EO⊥CO.又∵CO∩AB=O,∴EO⊥平面ABCD,又EO?平面EAB,∴平面EAB⊥平面ABCD.
(2)解 以AB中点O为坐标原点,分别以OC,OB,OE所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,

则A(0,-1,0),C(
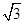 ,0,0),D
,0,0),D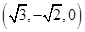 ,E(0,0,1).
,E(0,0,1).∴
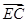 =(
=(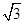 ,0,-1),
,0,-1),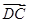 =(0,2,0),
=(0,2,0),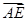 =(0,1,1).
=(0,1,1).设平面CDE的法向量n=(x,y,z),
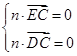
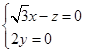 令z=1,解得
令z=1,解得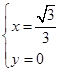
∴平面CDE的一个法向量n=
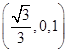 ,设直线AE与平面CDE所成角为θ.
,设直线AE与平面CDE所成角为θ.∴sin θ=
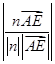 =
=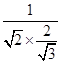 =
=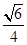 .
.∴直线AE与平面CDE所成角的正弦值是
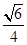 .
.
练习册系列答案
相关题目
 中,
中,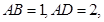 且
且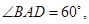 以
以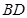 为折线,把
为折线,把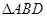 折起,使平面
折起,使平面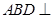 平面
平面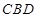 ,连接
,连接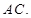
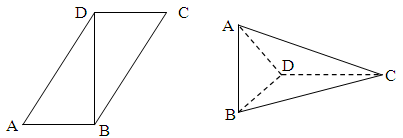
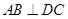 ;
;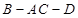 的余弦值.
的余弦值.
 的底面
的底面 是正方形,
是正方形, 底面
底面 是
是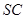 上的任意一点.
上的任意一点.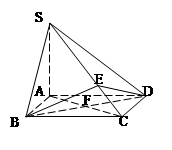
 平面
平面 ;
;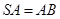 时,求二面角
时,求二面角 的大小.
的大小. ,
,

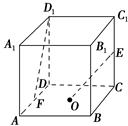




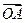 =(2,8),
=(2,8),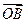 =(-7,2),则
=(-7,2),则
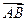 = .
= .