题目内容
15.已知在△ABC中,内角∠A、∠B、∠C的对边分别为a、b、c,且$\frac{b}{a+c}$=$\frac{a+b-c}{a+b}$.(1)求∠A;
(2)若b=5,$\overrightarrow{AC}$•$\overrightarrow{CB}$=5,求△ABC的面积.
分析 (1)整理原等式利用余弦定理求得cosA的值,进而求得A.
(2)利用向量的数量积运算公式和余弦定理求得a和c 关系式,与第一问中关系式求得c,进而利用三角形面积公式求得答案.
解答 解:(1)∵$\frac{b}{a+c}$=$\frac{a+b-c}{a+b}$,
∴ab+b2=a2+ab-ac+ac+bc-c2,
∴b2=a2+bc-c2,①
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∴A=$\frac{π}{3}$;
(2)$\overrightarrow{AC}$•$\overrightarrow{CB}$=|AC|•|CB|cosC=b•a•cosC=ab•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=5,
∴a2-c2=-15,②,
①②联立求得c=8,a=7,
∴三角形面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×5×8×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$.
点评 本题主要考查了余弦定理的运用,向量的数量积的运算公式的运用.解题过程中灵活运用边的关系,利用余弦定理建立方程求得即可.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
1.设a∈R,且(a-i)•2i(i为虚数单位)为正实数,则a等于( )
| A. | 1 | B. | 0 | C. | -1 | D. | 0或-1 |
6.设全集U是实数集R,M={x|x>2或x<-2},N={x|x≥3或x<1},则(∁UM)∩N是( )
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
20.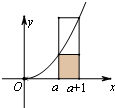 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | ln2 | D. | ln$\frac{5}{2}$ |
4.已知sinx+$\sqrt{3}$cosx=$\frac{8}{5}$,则cos($\frac{π}{6}$-x)=( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |