题目内容
14. 如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.(I)求证:AC⊥平面BCE;
(II)求三棱锥E-BCF的体积.
分析 (I)过C作CM⊥AB,垂足为M,利用勾股定理证明AC⊥BC,利用EB⊥平面ABCD,证明AC⊥EB,即可证明AC⊥平面BCE;
(II)证明CM⊥平面ABEF,利用VE-BCF=VC-BEF,即可求三棱锥E-BCF的体积.
解答 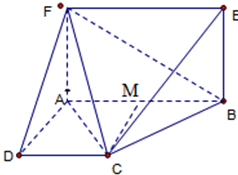 (I)证明:过C作CM⊥AB,垂足为M,
(I)证明:过C作CM⊥AB,垂足为M,
∵AD⊥DC,∴四边形ADCM为矩形,
∴AM=MB=2,
∵AD=2,AB=4,
∴AC=2$\sqrt{2}$,CM=2,BC=2$\sqrt{2}$
∴AB2=AC2+BC2,即AC⊥BC,
∵AF⊥平面ABCD,AF∥BE,
∴EB⊥平面ABCD,
∵AC?平面ABCD,∴AC⊥EB,
∵EB∩BC=B,
∴AC⊥平面BCE;
(II)解:∵AF⊥平面ABCD,
∴AF⊥CM,
∴CM⊥AB,AB∩AF=A,
∴CM⊥平面ABEF,
∴VE-BCF=VC-BEF=$\frac{1}{3}×\frac{1}{2}×BE×EF×CM$=$\frac{1}{6}×2×4×2$=$\frac{8}{3}$.
点评 本题考查了线面垂直的判定,三棱锥体积的计算,解答的关键是正确运用线面垂直的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知sinx+$\sqrt{3}$cosx=$\frac{8}{5}$,则cos($\frac{π}{6}$-x)=( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
2.设集合U={1,2,3,4,5},A={1,3},B={2,3,4},则(CUA)∩(CUB)=( )
| A. | {1} | B. | {5} | C. | {2,4} | D. | {1,2,4,5} |
6.设函数y=f(x)定义在实数集R上,则函数y=f(1-x)与y=f(x-1)的图象关于( )
| A. | 直线y=0对称 | B. | 直线x=0对称 | C. | 直线y=1对称 | D. | 直线x=1对称 |
3.函数f(x)=log2(x+2)-$\frac{3}{x}$(x>0)的零点所在的大致区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |