题目内容
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到点
到点![]() 的距离和它到直线
的距离和它到直线![]() 的距离相等,记点
的距离相等,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设点![]() 在曲线
在曲线![]() 上,
上,![]() 轴上一点
轴上一点![]() (在点
(在点![]() 右侧)满足
右侧)满足![]() ,若平行于
,若平行于![]() 的直线与曲线
的直线与曲线![]() 相切于点
相切于点![]() ,试判断直线
,试判断直线![]() 是否过点
是否过点![]() ?并说明理由.
?并说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 过点
过点![]() ,理由见解析
,理由见解析
【解析】
(1)由抛物线的定义求出![]() 的方程;
的方程;
(2)根据抛物线的定义表示出点![]() 的坐标,根据坐标写出直线
的坐标,根据坐标写出直线![]() 的斜率,进而得到直线
的斜率,进而得到直线![]() 的方程,将直线
的方程,将直线![]() 与抛物线方程联立,结合判别式得出
与抛物线方程联立,结合判别式得出![]() ,进而得出点D的坐标,求出直线
,进而得出点D的坐标,求出直线![]() 的斜率,讨论
的斜率,讨论![]() 和
和![]() ,得出直线
,得出直线![]() 的方程,即可判断直线
的方程,即可判断直线![]() 是否过点
是否过点![]() .
.
解:(1)根据抛物线的定义得,动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,直线
为焦点,直线![]() 的抛物线.
的抛物线.
![]()
(2)由题设![]() ,则
,则![]() ,
,
又![]() ,故
,故![]()
由于![]() ,则直线
,则直线![]() 不与
不与![]() 轴垂直
轴垂直
令平行于![]() 的直线
的直线![]() ,则
,则![]() ,
,
![]()
将直线![]() 代入
代入![]() ,得
,得![]() ,
,
整理![]() ……①
……①
![]() ,
,
![]()
当![]() 时,直线AB为
时,直线AB为![]() 轴,此时不存在平行于
轴,此时不存在平行于![]() 的直线与曲线
的直线与曲线![]() 相切于点
相切于点![]()
即![]()
![]()
所以①可以化为![]()
![]() ,
,![]() ,
,
![]()
当![]() 时
时
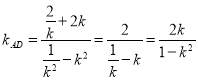
![]() ,
,
![]() ,过定点
,过定点![]()
当![]() 时,
时,![]() 也过点
也过点![]() ,故直线
,故直线![]() 过点
过点![]()

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】将标号为1,2,…,20的20张卡片放入下列表格中,一个格放入一张卡片.把每列标号最小的卡片选出,将这些卡片中标号最大的数设为a;把每行标号最大的卡片选出,将这些卡片中标号最小的数设为b.
甲同学认为a有可能比b大,乙同学认为a和b有可能相等.那么甲乙两位同学中说法正确的同学是_______.