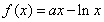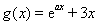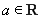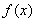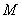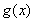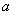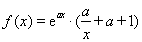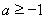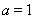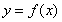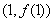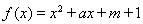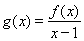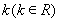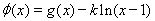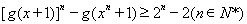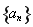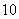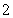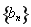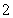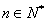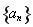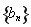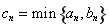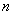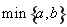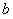题目内容
已知函数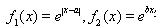
(I)若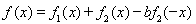 ,是否存在a,b
,是否存在a,b R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数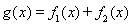 在R上的单调区间;
在R上的单调区间;
(III )对于给定的实数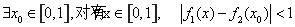 成立.求a的取值范围.
成立.求a的取值范围.
(I) 存在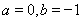 使
使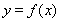 为偶函数〔II)
为偶函数〔II)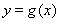 的增区间为
的增区间为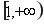 ,减区间为
,减区间为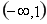 。(III )
。(III ) 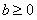 时,
时,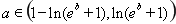 ;当
;当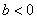 时,
时,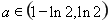
【解析】(Ⅰ)存在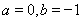 使
使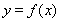 为偶函数,………………(2分)
为偶函数,………………(2分)
证明如下:此时: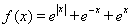 ,
,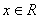
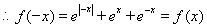 ,
,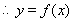 为偶函数。………………(4分)
为偶函数。………………(4分)
(注: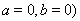 也可以)
也可以)
(Ⅱ)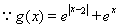 =
= ,………………(5分)
,………………(5分)
①当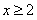 时
时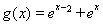 ,
,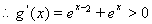
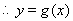 在
在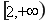 上为增函数。………………(6分)
上为增函数。………………(6分)
②当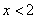 时
时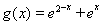 ,
,
则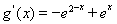 ,令
,令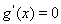 得到
得到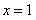 ,
,
(ⅰ)当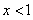 时
时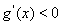 ,
,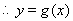 在
在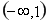 上为减函数。
上为减函数。
(ⅱ) 当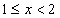 时
时 ,
,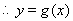 在
在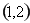 上为增函数。………………(8分)
上为增函数。………………(8分)
综上所述: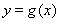 的增区间为
的增区间为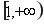 ,减区间为
,减区间为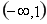 。………………(9分)
。………………(9分)
(Ⅲ)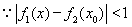 ,
,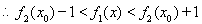
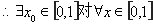 ,
,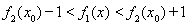 成立。
成立。
即: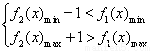 …………………………………………………(10分)
…………………………………………………(10分)
①当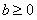 时,
时, 为增函数或常数函数,
为增函数或常数函数, 当
当 时
时
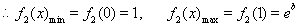
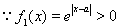
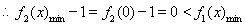 恒成立。
恒成立。
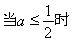

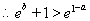
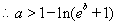
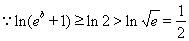
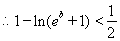
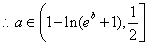
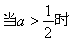
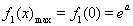
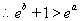
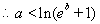
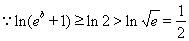
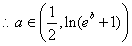
综上所述: ……………………………………………(12分)
……………………………………………(12分)
②当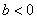 时,
时, 在[0,1]上为减函数,
在[0,1]上为减函数,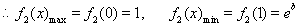
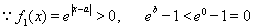
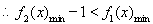 恒成立。
恒成立。
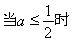

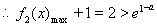
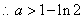

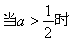
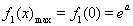

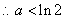
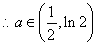
综上所述: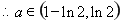 ……………………………………………(13分)
……………………………………………(13分)
由①②得当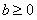 时,
时,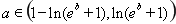 ;
;
当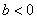 时,
时,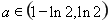 .……………………………………………(14分)
.……………………………………………(14分)

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目