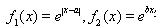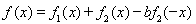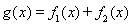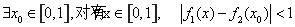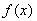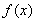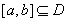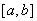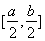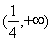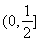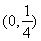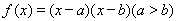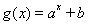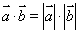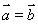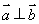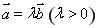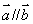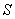题目内容
已知等差数列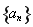 的首项为
的首项为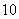 ,公差为
,公差为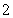 ,等比数列
,等比数列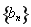 的首项为
的首项为 ,公比为
,公比为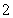 ,
,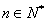 .
.
(1)求数列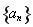 与
与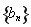 的通项公式;
的通项公式;
(2)设第 个正方形的边长为
个正方形的边长为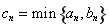 ,求前
,求前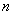 个正方形的面积之和
个正方形的面积之和 .
.
(注: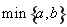 表示
表示 与
与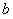 的最小值.)
的最小值.)
(1)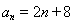 ,
,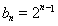 ;(2)
;(2)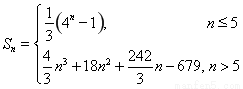 .
.
【解析】
试题分析:(1)利用等差数列和等比数列的通项公式分别求出数列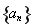 与
与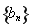 的通项公式;(2)先利用作差法确定
的通项公式;(2)先利用作差法确定 与
与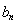 的大小,在比较两者的大小是,一是利用数学归纳法,方法二是利用二项式定理,确定数列
的大小,在比较两者的大小是,一是利用数学归纳法,方法二是利用二项式定理,确定数列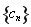 的通项公式(用分段数列的形式来进行表示,然后对
的通项公式(用分段数列的形式来进行表示,然后对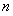 的取值进行分类讨论,进而求出
的取值进行分类讨论,进而求出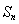 .
.
试题解析:(1)由于数列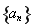 是以
是以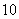 为首项,以
为首项,以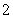 为公差的等差数列,所以
为公差的等差数列,所以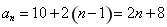 ,
,
又因为数列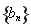 是以
是以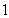 为首项,以
为首项,以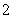 为公比的等比数列,因此
为公比的等比数列,因此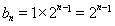 ;
;
2)因为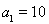 ,
,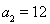 ,
,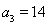 ,
,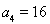 ,
,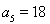 ,
,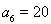 ,
,
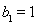 ,
,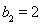 ,
,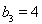 ,
,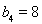 ,
,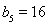 ,
,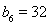 ,
,
易知当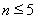 时,
时,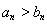 ,
,
下面证明当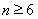 时,不等式
时,不等式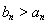 成立.
成立.
方法1:(i)当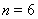 时,
时,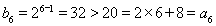 ,不等式显然成立,
,不等式显然成立,
(ii)假设当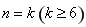 时,不等式成立,即
时,不等式成立,即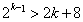 ,
,
则有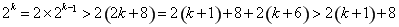 ,
,
这说明当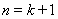 时,不等式也成立,
时,不等式也成立,
综合(i)(ii)可知,不等式对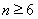 的所有整数都成立.
的所有整数都成立.
所以当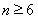 时,
时,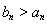 ;
;
方法2:因为当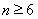 时,
时,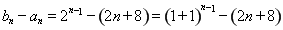
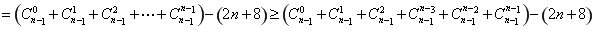
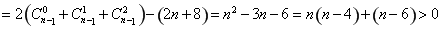 ,
,
所以当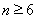 时,
时,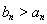 ,所以
,所以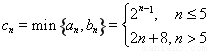 ,
,
则 ,
,
当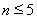 时,
时,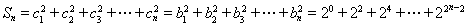
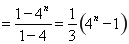 ,
,
当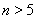 时,
时,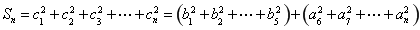
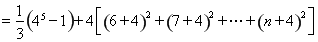
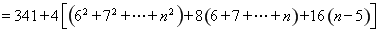
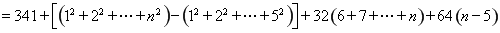
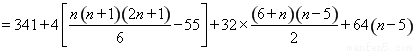
 .
.
综上可知,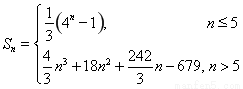 .
.
考点:1.等差数列与等比数列的通项公式;2.利用作差啊比较大小;3.数学归纳法;4二项式定理;5.数列求和

练习册系列答案
相关题目
某农场给某种农作物施肥量x(单位:吨)与其产量y(单位:吨)的统计数据如下表:
施肥量x | 2 | 3 | 4 | 5 |
产量y | 26 | 39 | 49 | 54 |
根据上表,得到回归直线方程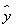 =9.4x+
=9.4x+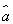 ,当施肥量x=6时,该农作物的预报产量是________.
,当施肥量x=6时,该农作物的预报产量是________.