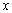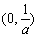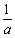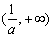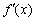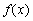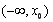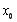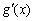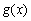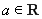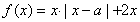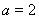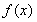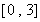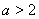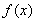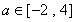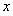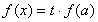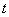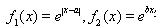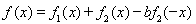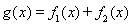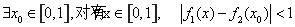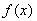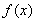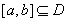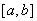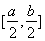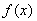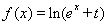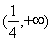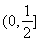题目内容
已知函数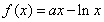 ,
,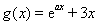 ,其中
,其中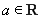 .
.
(Ⅰ)求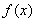 的极值;
的极值;
(Ⅱ)若存在区间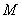 ,使
,使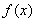 和
和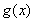 在区间
在区间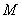 上具有相同的单调性,求
上具有相同的单调性,求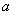 的取值范围.
的取值范围.
(Ⅰ)极小值为 ;没有极大值(Ⅱ)
;没有极大值(Ⅱ)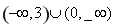
【解析】(Ⅰ)【解析】 的定义域为
的定义域为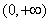 ,………………1分
,………………1分
且 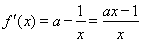 . ………………2分
. ………………2分
① 当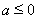 时,
时,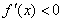 ,故
,故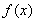 在
在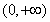 上单调递减.
上单调递减.
从而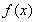 没有极大值,也没有极小值. ………………3分
没有极大值,也没有极小值. ………………3分
② 当 时,令
时,令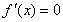 ,得
,得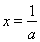 .
.
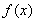 和
和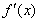 的情况如下:
的情况如下:
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
故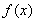 的单调减区间为
的单调减区间为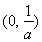 ;单调增区间为
;单调增区间为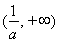 .
.
从而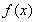 的极小值为
的极小值为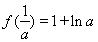 ;没有极大值.………………5分
;没有极大值.………………5分
(Ⅱ)【解析】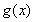 的定义域为
的定义域为 ,且
,且 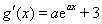 .………………6分
.………………6分
③ 当 时,显然
时,显然 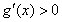 ,从而
,从而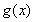 在
在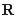 上单调递增.
上单调递增.
由(Ⅰ)得,此时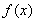 在
在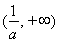 上单调递增,符合题意. ………………8分
上单调递增,符合题意. ………………8分
④ 当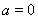 时,
时,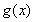 在
在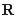 上单调递增,
上单调递增,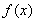 在
在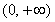 上单调递减,不合题意.……9分
上单调递减,不合题意.……9分
⑤ 当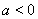 时,令
时,令 ,得
,得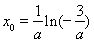 .
.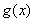 和
和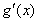 的情况如下表:
的情况如下表:
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
当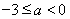 时,
时,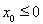 ,此时
,此时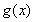 在
在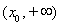 上单调递增,由于
上单调递增,由于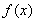 在
在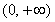 上单调递减,不合题意. ………………11分
上单调递减,不合题意. ………………11分
当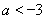 时,
时,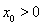 ,此时
,此时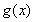 在
在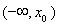 上单调递减,由于
上单调递减,由于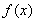 在
在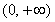 上单调递减,符合题意.
上单调递减,符合题意.
综上, 的取值范围是
的取值范围是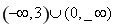 . ………………13
. ………………13

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目